User:Airman72

For molecules that are non attracting hard spheres, $a=0$, the vdW virial expansion becomes simply $Z=(1-b\rho )^{-1}=\sum _{i=0}^{\infty }(b\rho )^{i}$, which illustrates the effect of the excluded volume alone. It was recognized early on that this was in error beginning with the term $(b\rho )^{2}$. Boltzmann calculated its correct value as $(5/8)(b\rho )^{2}$, and used the result to propose an enhanced version of the vdW equation

$$(p+a/v^{2})(v-b/3)=RT[1+2b/(3v)+7b^{2}/(24v^{2})].$$

On expanding $(v-b/3)^{-1}$, this produced the correct coefficients thru $(b/v)^{2}$ and also gave infinite pressure at $b/3$, which is approximately the close packing distance for hard spheres. This was one of the first of many equations of state proposed over the years that attempted to make quantitative improvements to the remarkably accurate explanations of real gas behavior produced by the vdW equation.

Mixtures

In 1890 van der Waals published an article that initiated the study of fluid mixtures. It was subsequently included as Part III of a later published version of his thesis. His essential idea was that in a binary mixture of vdw fluids described by the equations

$$p_{1}={\frac {RT}{v-b_{11}}}-{\frac {a_{11}}{v^{2}}}\quad {\mbox{and}}\quad p_{2}={\frac {RT}{v-b_{22}}}-{\frac {a_{22}}{v^{2}}}$$

the mixture is also a vdW fluid given by

$$p={\frac {RT}{v-b_{x}}}-{\frac {a_{x}}{v^{2}}}$$

where

$$a_{x}=a_{11}x_{1}^{2}+2a_{12}x_{1}x_{2}+a_{22}x_{2}^{2}\quad {\mbox{and}}\quad b_{x}=b_{11}x_{1}^{2}+2b_{12}x_{1}x_{2}+b_{22}x_{2}^{2}$$

Here $x_{1}=N_{1}/N$, and $x_{2}=N_{2}/N$, with $N=N_{1}+N_{2}$ (so that $x_{1}+x_{2}=1$) are the mole fractions of the two fluid substances. Adding the equations for the two fluids shows that $p\neq p_{1}+p_{2}$, although for $v$ sufficiently large $p\approx p_{1}+p_{2}$ with equality holding in the ideal gas limit. The quadratic forms for $a_{x}$ and $b_{x}$ are a consequence of the forces between molecules. This was first shown by Lorentz, and was credited to him by van der Waals. The quantities $a_{11},\,a_{22}$ and $b_{11},\,b_{22}$ in these expressions characterize collisions between two molecules of the same fluid component while $a_{12}=a_{21}$ and $b_{12}=b_{21}$ represent collisions between one molecule of each of the two different component fluids. This idea of van der Waals was later called a one fluid model of mixture behavior.

Assuming that $b_{12}$ is the arithmetic mean of $b_{11}$ and $b_{22}$, $b_{12}=(b_{11}+b_{22})/2$, substituting into the quadratic form, and noting that $x_{1}+x_{2}=1$ produces

$$b=b_{11}x_{1}+b_{22}x_{2}$$

Van der Waals wrote this relation, but did not make use of it initially. However, it has been used frequently in subsequent studies, and its use is said to produce good agreement with experimental results at high pressure.

In this article van der Waals used the Helmholtz Potential Minimum Principle to establish the conditions of stability. This principle states that in a system in diathermal contact with a heat reservoir $T=T_{R}$, $DF=0$ and $D^{2}F>0$, namely at equilibrium the Helmholtz potential is a minimimum. This leads to the requirement $\partial ^{2}f/\partial v^{2}|_{T}=-\partial p/\partial v|_{T}>0$, which is the previous stability condition for the pressure, but in addition requires that the curvature of $f=FN_{\mbox{A}}/N$ is positive at a stable state.

For a single substance the definition of the molar Gibbs free energy can be written in the form $f=g-pv$. Thus when $p$ and $g$ are constant along with temperature the function $f(T_{R},v)$ represents a straight line with slope $-p$, and intercept $g$. Since the curve, $f(T_{R},v)$, has positive curvature everywhere when $T_{R}\geq T_{c}$, the curve and the straight line will be have a single tangent. However, for a subcritical, $T_{R}$, with $p=p_{s}(T_{R})$ and a suitable value of $g$ the line will be tangent to $f(T_{R},v)$ at the molar volume of each coexisting phase, saturated liquid, $v_{f}(T_{R})$, and saturated vapor, $v_{g}(T_{R})$; there will be a double tangent. Furthermore, each of these points is characterized by the same value of $g$ as well as the same values of $p$ and $T_{R}$. These are the same three specifications for coexistence that were used previously.

Figure 8: The straight line (dotted-solid black) is tangent to the curve $f_{r}(0.875,v_{r})$ (solid-dashed green, dotted gray) at the two points $v_{rf}=0.576$ and $v_{rg}=2.71$. The slope of the straight line, given by $\partial _{v_{r}}f_{r}=-p_{c}v_{c}/(RT_{c})p_{rs}$, is $-0.215$ corresponding to $p_{rs}=0.5730$. All this is consistent with the data of the green curve, $T_{r}=7/8$, of Fig. 1. The intercept on the line is $g$, but its numerical value is arbitrary due to a constant of integration.

As depicted in Fig. 8, the region on the green curve $f(T_{R},v)$ for $v\leq v_{f}$ ($v_{f}$ is designated by the left green circle) is the liquid. As $v$ increases past $v_{f}$ the curvature of $f$ (proportional to $\partial _{v^{2}}^{2}f=-\partial _{v}p$) continually decreases. The point characterized by $\partial _{v^{2}}^{2}f=-\partial _{v}p=0$, is a spinodal point, and between these two points is the metastable superheated liquid. For further increases in $v$ the curvature decreases to a minimum then increases to another spinodal point; between these two spinodal points is the unstable region in which the fluid cannot exist in a homogeneous equilibrium state. With a further increase in $v$ the curvature increases to a maximum at $v_{g}$, where the slope is $p_{s}$; the region between this point and the second spinodal point is the metastable subcooled vapor. Finally, the region $v\geq v_{g}$ is the vapor. In this region the curvature continually decreases until it is zero at infinitely large $v$. The double tangent line is rendered solid between its saturated liquid and vapor values to indicate that states on it are stable, as opposed to the metastable and unstable states, above it (with larger Helmholtz free energy), but black, not green, to indicate that these states are heterogeneous, not homogeneous solutions of the vdW equation.

For a vdW fluid the molar Helmholtz potential is simply

$$f_{r}=u_{r}-T_{r}s_{r}={\mbox{C}}_{u}+T_{r}\{c-{\mbox{C}}_{s}-\ln[T_{r}^{c}(3v_{r}-1)]\}-9/(8v_{r})$$

where $f_{r}=f/(RT_{c})$. A plot of this function for the suncritical isotherm $T_{r}=7/8$ is the one shown in Fig. 8 along with the line tangent to it at its two coexisting saturation points. The data illustrated in Fig. 8 is exactly the same as that shown in Fig.1 for this isotherm.

Van der Waals introduced the Helmholtz function because its properties could be easily extended to the binary fluid situation. In a binary mixture of vdW fluids the Helmholtz potential is a function of 2 variables, $f(T_{R},v,x)$, where $x$ is a composition variable, for example $x=x_{2}$ so $x_{1}=1-x$. In this case there are three stability conditions

$${\frac {\partial ^{2}f}{\partial v^{2}}}>0\qquad {\frac {\partial ^{2}f}{\partial x^{2}}}>0\qquad {\frac {\partial ^{2}f}{\partial v^{2}}}{\frac {\partial ^{2}f}{\partial x^{2}}}-\left({\frac {\partial ^{2}f}{\partial x\partial v}}\right)^{2}>0$$

and the Helmholtz potential is a surface (of physical interest in the region $0\leq x\leq 1$). The first two stability conditions show that the curvature in each of the directions $v$ and $x$ are both positive for stable states while the third condition indicates that stable states correspond to elliptic points on this surface. Moreover its limit, $\partial _{x^{2}}^{2}f\partial _{v^{2}}^{2}f-(\partial _{xv}^{2}f)^{2}=0$, is in this case the specification of spinodal points.

For a binary mixture the Euler equation, can be written in the form

$$f=-pv+\mu _{1}x_{1}+\mu _{2}x_{2}=-pv+(\mu _{2}-\mu _{1})x+\mu _{1}$$

Here $\mu _{j}=\partial _{x_{j}}f$ are the molar chemical potentials of each substance, $j=1,2$. For $p$, $\mu _{1}$ and $\mu _{2}$, all constant this is the equation of a plane with slopes $-p$ in the $v$ direction, $\mu _{2}-\mu _{1}$ in the $x$ direction, and intercept $\mu _{1}$. As in the case of a single substance, here the plane and the surface can have a double tangent and the locus of the coexisting phase points forms a curve on each surface. The coexistence conditions are that the two phases have the same $T$, $p$, $\mu _{2}-\mu _{1}$, and $\mu _{1}$; the last two are equivalent to having the same $\mu _{1}$ and $\mu _{2}$ individually, which are just the Gibbs conditions for material equilibrium in this situation. Although this case is similar to the previous one of a single component, here the geometry can be much more complex. The surface can develop a wave (called a plait or fold in the literature) in the $x$ direction as well as the one in the $v$ direction. Therefore, there can be two liquid phases that can be either miscible, or wholly or partially immiscible, as well as a vapor phase. Despite a great deal of both theoretical and experimental work on this problem by van der Waals and his successors, work which produced much useful knowledge about the various types of phase equilibria that are possible in fluid mixtures, complete solutions to the problem were only obtained after 1967, when the availability of modern computers made calculations of mathematical problems of this complexity feasible for the first time. The results obtained were, in Rowlinson's words,

a spectacular vindication of the essential physical correctness of the ideas behind the van der Waals equation, for almost every kind of critical behavior found in practice can be reproduced by the calculations, and the range of parameters that correlate with the different kinds of behavior are intelligible in terms of the expected effects of size and energy.

In order to obtain these numerical results the values of the constants of the individual component fluids $a_{11},a_{22},b_{11},b_{22}$ must be known. In addition, the effect of collisions between molecules of the different components, given by $a_{12}$ and $b_{12}$, must also be specified. In he absence of experimental data, or computer modelling results to estimate their value, the empirical combining laws,

$$a_{12}=(a_{11}a_{22})^{1/2}\qquad {\mbox{and}}\qquad b_{12}^{1/3}=(b_{11}^{1/3}+b_{22}^{1/3})/2,$$

the geometric and algebraic means respectively can be used. These relations correspond to the empirical combining laws for the intermolecular force constants,

$$\epsilon _{12}=(\epsilon _{11}\epsilon _{22})^{1/2}\qquad {\mbox{and}}\qquad \sigma _{12}=(\sigma _{11}+\sigma _{22})/2,$$

the first of which follows from a simple interpretation of the dispersion forces in terms of polarizabilities of the individual molecules while the second is exact for rigid molecules. Then, generalizing for $n$ fluid components, and using these empirical combinig laws, the expressions for the material constants are:

$$a_{x}=\sum _{i=1}^{n}\sum _{j=1}^{n}(a_{ii}a_{jj})^{1/2}x_{i}x_{j}\quad {\mbox{which can be written as}}\quad a_{x}={\Big (}\sum _{i=1}^{n}a_{ii}^{1/2}x_{i}{\Big )}^{2}$$

$$b_{x}=(1/8)\sum _{i=1}^{n}\sum _{j=1}^{n}(b_{ii}^{1/3}+b_{jj}^{1/3})^{3}x_{i}x_{j}$$

Using these expressions in the vdW equation is apparently helpful for divers, as well as being important for physicists, physical chemists, and chemical engineers in their study and management of the various phase equilibria and critical behavior observed in fluid mixtures.

Another method of specifying the vdW constants pioneered by W.B. Kay, and known as Kay's rule. specifies the effective critical temperature and pressure of the fluid mixture by

$$T_{cx}=\sum _{i=1}^{n}T_{ci}x_{i}\qquad {\mbox{and}}\qquad p_{cx}=\sum _{i=1}^{n}\,p_{ci}x_{i}$$

In terms of these quantities the vdW mixture constants are then,

$$a_{x}={\frac {27}{64}}{\frac {(RT_{cx})^{2}}{p_{cx}}}\qquad \qquad b_{x}={\frac {1}{8}}{\frac {RT_{cx}}{p_{cx}}}$$

and Kay used these specifications of the mixture critical constants as the basis for calculations of the thermodynamic properties of mixtures.

Kay's idea was adopted by T. W. Leland, who applied it to the molecular parameters, $\epsilon ,\sigma$, which are related to $a,b$ through $T_{c},p_{c}$ by $a\propto \epsilon \sigma ^{3}$ and $b\propto \sigma ^{3}$ (see the introduction to this article). Using these together with the quadratic form of $a,b$ for mixtures produces

$$\sigma _{x}^{3}=\sum _{i=i}^{n}\sum _{j=1}^{n}\,\sigma _{ij}^{3}x_{i}x_{j}\qquad {\mbox{and}}\qquad \epsilon _{x}=\left[\sum _{i=1}^{n}\sum _{j=1}^{n}\epsilon _{ij}\sigma _{ij}^{3}x_{i}x_{j}\right]\left[\sum _{i=i}^{n}\sum _{j=1}^{n}\,\sigma _{ij}^{3}x_{i}x_{j}\right]^{-1}$$

which is the van der Waals approximation expressed in terms of the intermolecular constants. This approximation, when compared with computer simulations for mixtures, are in good agreement over the range $1/2<(\sigma _{11}/\sigma _{22})^{3}<2$, namely for molecules of not too different diameters. In fact Rowlinson said of this approximation, "It was, and indeed still is, hard to improve on the original van der Waals recipe when expressed in [this] form".

Mathematical Validity and Utility

The vdW equation, characterized by the 3 constants $a,b,R$, cannot represent real fluids. If it did they would all have the same saturation curve as shown in Fig. 2., but that is not the actual case as shown in Figs. 3 and 4; van der Waals was aware of this when he published the result. Therefore the vdW equation cannot be rigorously derived, although as Goodstein has noted "[m]any derivations, pseudo-derivations, and plausibility arguments have been given..." for it.

What has been rigorously demonstrated by using the canonical ensemble of statistical mechanics applied to a moderately dense gas,

$${\cal {Z}}={\frac {Q_{N}}{N!\,\Lambda ^{3N}}}\qquad {\mbox{where}}\qquad Q_{N}=\int _{V^{\bf {N}}}\,\exp \left[-{\frac {\Phi ({\bf {r^{N}}})}{kT}}\right]\,d{\bf {r^{N}}}$$

($\Lambda$ is the DeBroglie wavelength and $Q_{N}$ is the configuration integral), and regarding $\Phi ({\bf {r^{N}}})=\sum \sum q(r_{ij})+\sum \sum w(r_{ij})$ to be the sum of short-range repulsive parts $q(r/\sigma )$ and long-range attractive parts $w=-(\sigma /\ell )^{3}\varphi \{-r/\ell \}$, is that in a suitable limiting process ($\ell ,N,V\rightarrow \infty$ such that $N/V=\rho$ is finite and $\ell \ll V^{1/3}$), in which the attractive part of the intermolecular potential becomes infinitely weak and infinitely long-range, the limit of $p(\rho ,T,\ell )$ is the vdW equation including the Maxwell condition.

Mathematical details

In terms of the right ascension of the Sun, α, and that of a mean Sun moving uniformly along the celestial equator, α_M, the equation of time is defined as the difference, Δt = α_M - α. In this expression Δt is the time difference between apparent solar time (time measured by a sundial) and mean solar time (time measured by a mechanical clock). The left side of this equation is a time difference while the right side terms are angles; however, astronomers regard time and angle as quantities that are related by conversion factors such as; 2π radian = 360° = 1 day = 24 hour. The difference, Δt, is measureable because α can be measured and α_M, by definition, is a linear function of mean solar time.

The equation of time can be calculated based on Newton's theory of celestial motion in which the earth and sun describe elliptical orbits about their common mass center. In doing this it is usual to write α_M = 2πt/t_Y = Λ where

• t is dynamical time, the independent variable in the theory,
• t_Y is the length of time in a tropical year,
• Λ is the ecliptic longitude of a dynamical mean Sun; the angle from the vernal equinox to a fictitious Sun moving uniformly along the ecliptic and coinciding with the apparent sun at apoapsis and periapsis.

Substituting α_M into the equation of time, it becomes

$\Delta t=\Lambda -\alpha =M+\lambda _{p}-\alpha$

The new angles appearing here are:

• M is the mean anomaly; the angle from the periapsis to the dynamical mean Sun,
• λ_p = Λ - M = 4.9412 = 283.11° is the ecliptic longitude of the periapsis written with its value on 1 Jan 2010 at 12 noon.

However, the displayed equation is approximate; it is not accurate over very long times because it ignores the distinction between dynamical time and mean solar time. In addition, an elliptical orbit formulation ignores small perturbations due to the moon and other planets. Another complication is that the orbital parameter values change significantly over long times, for example λ_p increases by about 1.7 degrees per century. Consequently, calculating Δt using the displayed equation with constant orbital parameters produces accurate results only for sufficiently short times (decades). It is possible to write an expression for the equation of time that is valid for centuries, but it is necessarily much more complex.

In order to calculate α, and hence Δt, as a function of M, three additional angles are required; they are

• E the Sun's eccentric anomaly,
• ν the Sun's true anomaly,
• λ = ν + λ_p the Sun's true longitude on the ecliptic.

The celestial sphere and the Sun's elliptical orbit as seen by a geocentric observer looking normal to the ecliptic showing the 6 angles (M, λ_p, α, ν, λ, E) needed for the calculation of the equation of time. For the sake of clarity the drawings are not to scale.

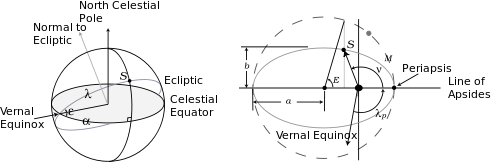
All these angles are shown in the figure on the right, which shows the celestial sphere and the Sun's elliptical orbit seen from the Earth (the same as the Earth's orbit seen from the Sun). In this figure ε = 0.40907 = 23.438° is the obliquity, while e = [1 − (b/a)²]^1/2 = 0.016705 is the eccentricity of the ellipse.

Now given a value of 0≤M≤2π, one can calculate α(M) by means of the following procedure:

First, knowing M, calculate E from Kepler's equation

$M=E-e\sin E$

A numerical value can be obtained from an infinite series, graphical, or numerical methods. Alternatively, note that for e = 0, E = M, and for small e, by iteration, E ~ M + e sin M. This can be improved by iterating again, but for the small value of e that characterises the orbit this approximation is sufficient.

Next, knowing E, calculate the true anomaly ν from an elliptical orbit relation

$\nu =2\tan ^{-1}\left[{\sqrt {\frac {1+e}{1-e}}}\tan {\frac {E}{2}}\right]$

The correct branch of the multiple valued function tan⁻¹x to use is the one that makes ν a continuous function of E(M) starting from ν(E=0) = 0. Thus for 0≤ E < π use tan⁻¹x = Tan⁻¹x, and for π < E ≤ 2π use tan⁻¹x = Tan⁻¹x + π. At the specific value E = π for which the argument of tan is infinite, use ν = E. Here Tan⁻¹x is the principal branch, |Tan⁻¹x| < π/2; the function that is returned by calculators and computer applications. Alternatively, note that for e = 0, ν = E and for small e, from a one term Taylor expansion, ν ~ E+e sin E ~ M +2 e sin M.

Next knowing ν calculate λ from its definition above

$\lambda =\nu +\lambda _{p}$

The value of λ varies non-linearly with M because the orbit is elliptical, from the approximation for ν, λ ~ M + λ_p + 2 e sin M.

Next, knowing λ calculate α from a relation for the right triangle on the celestial sphere shown above

$\alpha =\tan ^{-1}[\cos \varepsilon \,\tan \lambda ]$

Like ν previously, here the correct branch of tan⁻¹x to use makes α a continuous function of λ(M) starting from α(λ=0)=0. Thus for (2k-1)π/2 < λ < (2k+1)π/2, use tan⁻¹x = Tan⁻¹x + kπ, while for the values λ = (2k+1)π/2 at which the argument of tan is infinite use α = λ. Since λ_p ≤ λ ≤ λ_p+ 2π when M varies from 0 to 2π, the values of k that are needed, with λ_p = 4.9412, are 2, 3, and 4. Although an approximate value for α can be obtained from a one term Taylor expansion like that for ν, it is more efficatious to use the equation sin(α - λ) = - tan²(ε/2) sin(α + λ). Note that for ε = 0, α = λ and for small ε, by iteration, α ~ λ - tan²(ε/2) sin 2λ ~ M + λ_p + 2e sin M - tan²(ε/2) sin(2M+2λ_p).

Finally, Δt can be calculated using the starting value of M and the calculated α(M). The result is usually given as either a set of tabular values, or a graph of Δt as a function of the number of days past periapsis, n, where 0≤n≤ 365.242 (365.242 is the number of days in a tropical year); so that

$M={\frac {2\pi \,n}{365.242}}$

Using the approximation for α(M), Δt can be written as a simple explicit expression, which is designated Δt_a because it is only an approximation.

$\Delta t_{a}=-2e\sin M+\tan ^{2}{\frac {\varepsilon }{2}}\,\sin(2M+2\lambda _{p})=[-7.657\sin M+9.862\sin(2M+3.599)]{\mbox{min}}$

The equation of time as calculated by the exact procedure for Δt described in the text and the asymptotic expression for Δt_a given there.

This equation was first derived by Milne, who wrote it in terms of Λ = M + λ_p. The numerical values written here result from using the orbital parameter values for e, ε, and λ_p given previously in this section. When evaluating the numerical expression for Δt_a as given above, a calculator must be in radian mode to obtain correct values. Note also that the date and time of periapsis (perihelion of the Earth orbit) varies from year to year; a table giving the connection can be found in perihelion.

A comparative plot of the two calculations is shown in the figure on the right. The approximate calculation is seen to be close to the exact one, the absolute error, Err = |(Δt− Δt_a)|, is less than 45 seconds throughout the year; its largest value is 44.8 sec and occurs on day 273. More accurate approximations can be obtained by retaining higher order terms , but they are necessarily more time consuming to evaluate. At some point it is simpler to just evaluate Δt, but Δt_a as written above is easy to evaluate, even with a calculator, and has a nice physical explanation as the sum of two terms, one due to obliquity and the other to eccentricity. This is not true either for Δt considered as a function of M or for higher order approximations of Δt_a.

References

• Burington R S 1949 Handbook of Mathematical Tables and Formulas (Sandusky, Ohio: Handbook Publishers)
• Duffett-Smith P 1988 Practical Astronomy with your Calculator Third Edition (Cambridge: Cambridge University Press)
• Heilbron J L 1999 The Sun in the Church, (Cambridge Mass: Harvard University Press|isbn=0-674-85433-0)
• Hinch E J 1991 Perturbation Methods, (Cambridge: Cambridge University Press)
• Hughes D W, et al. 1989, The Equation of Time, Monthly Notices of the Royal Astronomical Society 238 pp 1529-1535
• Meeus, J 1997 Mathematical Astronomy Morsels, (Richmond, Virginia: Willman-Bell)
• Milne R M 1921, Note on the Equation of Time, The Mathematical Gazette 10 (The Mathematical Association) pp 372–375
• Moulton F R 1970 An Introduction to Celestial Mechanics, Second Revised Edition, (New York: Dover)
• Muller M 1995, "Equation of Time - Problem in Astronomy", Acta Phys Pol A 88 Supplement, S-49.
• Roy A E 1978 Orbital Motion, (Adam Hilger|ISBN=0-85274-228-2)
• Whitman A M 2007, "A Simple Expression for the Equation of Time", Journal Of the North American Sundial Society 14 pp 29–33