Covering space: Difference between revisions
Rescuing 1 sources and tagging 0 as dead.) #IABot (v2.0.8.6) (Whoop whoop pull up - 9541 |
No edit summary Tags: nowiki added Visual edit |
||
| Line 1: | Line 1: | ||
A covering of a [[topological space]] <math>X</math> is a [[continuous map]] <math>\pi : E \rightarrow X</math> with special properties. |
|||
{{Short description|A topological space that maps onto another, looking locally like separate copies}} |
|||
{{more citations needed|date=June 2012}} |
|||
== Definition == |
|||
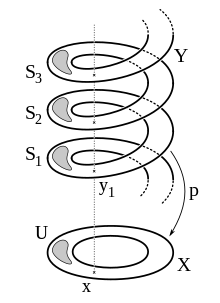
[[File:Covering space diagram.svg|thumb|250px|right|A covering map satisfies the local triviality condition. Intuitively, such maps locally project a "stack of pancakes" above an [[open set|open region]], ''U'', onto ''U''.]] |
|||
Let <math>X</math> be a topological space. A '''covering''' of <math>X</math> is a continuous map |
|||
: <math> \pi : E \rightarrow X</math> |
|||
In [[mathematics]], specifically [[algebraic topology]], a '''covering map''' (also '''covering projection''') is a [[continuous function]] <math>p</math> from a [[topological space]] <math>C</math> to a topological space |
|||
<math>X</math> such that each point in <math>X</math> has an [[Neighborhood_(mathematics)#Definitions|open neighborhood]] '''evenly covered''' by <math>p</math> (as shown in the image).<ref>{{harvnb|Spanier|1994|p=[https://books.google.com/books?id=h-wc3TnZMCcC&pg=PA62 62]}}</ref> In this case, <math>C</math> is called a '''covering space''' and <math>X</math> the '''base space''' of the covering projection. The definition implies that every covering map is a [[local homeomorphism]]. |
|||
s.t. there exists a [[discrete space]] <math>D</math> and for every <math>x \in X</math> an [[Neighbourhood (mathematics)|open neighborhood]] <math>U \subset X</math>, s.t. <math>\pi^{-1}(U)= \displaystyle \bigsqcup_{d \in D} V_d </math> and <math>\pi|_{V_d}:V_d \rightarrow U </math> is a [[homeomorphism]] for every <math>d \in D </math>.[[File:Covering space diagram.svg|thumb|220x220px|Intuitively, a covering locally project a "stack of pancakes" above an [[open neighborhood]] <math>U</math> onto <math>U</math>]] |
|||
Covering spaces play an important role in [[homotopy theory]], [[harmonic analysis]], [[Riemannian geometry]] and [[differential topology]]. In Riemannian geometry for example, [[Ramification (mathematics)#In algebraic topology|ramification]] is a generalization of the notion of covering maps. Covering spaces are also deeply intertwined with the study of homotopy groups and, in particular, the [[fundamental group]]. An important application comes from the result that, if <math>X</math> is a "sufficiently good" [[topological space]], there is a [[bijection]] between the collection of all [[isomorphism class]]es of [[connected space|connected]] coverings of <math>X</math> and the [[conjugacy class]]es of [[subgroup]]s of the [[fundamental group]] of <math>X</math>. |
|||
Often, the notion of a covering is used for the '''covering space''' <math>E</math> as well as for the map <math> \pi : E \rightarrow X</math>. The open sets <math>V_{d}</math> are called '''sheets,''' which are uniquely determined if <math>U</math> is [[Connected space|connected]].<ref name="Hatcher">{{Cite book|last=Hatcher|first=Allen|title=Algebraic Topology|publisher=Cambridge Univ. Press|year=2001|isbn=0-521-79160-X|location=Cambridge}}</ref><math>\,^{p.56}</math> For a <math>x \in X</math> the discrete subset <math>\pi^{-1}(x)</math> is called the '''fiber''' of <math>x</math>. The '''degree''' of a covering is the [[cardinality]] of the space <math>D</math>. If <math>E</math> is [[Path connected|path-connected]], then the covering <math> \pi : E \rightarrow X</math> is denoted as a '''path-connected covering'''. |
|||
== |
== Examples == |
||
Let <math>X</math> be a [[topological space]]. A '''covering space''' of <math>X</math> is a topological space <math>C</math> together with a [[continuous function (topology)|continuous]] [[surjective]] map |
|||
* For every topological space <math>X</math> there exists the covering <math>\pi:X \rightarrow X</math> with <math>\pi(x)=x</math>, which is denoted as the trivial covering of <math>X.</math> |
|||
:<math>p \colon C \to X</math> |
|||
[[File:Covering_map.svg|thumb|The space <math>Y=[0,1] \times \mathbb{R}</math> is the covering space of <math>X=[0,1] \times S^1</math>. The disjoint open sets <math>S_i</math> are mapped homeomorphically onto <math>U</math>. The fiber of <math>x</math> consists of the points <math>y_i</math>.]] |
|||
* The map <math>r \colon \mathbb{R} \to S^1</math> with <math>r(t)=(\cos(2 \pi t), \sin(2 \pi t))</math> is a covering of the [[unit circle]] <math>S^1</math>. For an open neighborhood <math>U \subset X</math> of an <math>x \in S^1</math>, which has positiv <math>\cos(2 \pi t)</math>-value, one has: <math>r^{-1}(U)=\displaystyle\bigsqcup_{n \in \mathbb{Z}} ( n - \frac 1 4, n + \frac 1 4)</math>. |
|||
* Another covering of the unit circle is the map <math>q \colon S^1 \to S^1</math> with <math>q(z)=z^{n}</math> for some <math>n \in \mathbb{N}</math>. For an open neighborhood <math>U \subset X</math> of an <math>x \in S^1</math>, one has: <math>q^{-1}(U)=\displaystyle\bigsqcup_{i=1}^{n} U</math>. |
|||
* A map which is a [[local homeomorphism]] but not a covering of the unit circle is <math>p \colon \mathbb{R_{+}} \to S^1</math> with <math>p(t)=(\cos(2 \pi t), \sin(2 \pi t))</math>. There is a sheet of an open neighborhood of <math>(1,0)</math>, which is not mapped homeomorphically onto <math>U</math>. |
|||
== Properties == |
|||
such that for every <math>x \in X</math>, there exists an [[Neighbourhood_(mathematics)#Definitions|open neighborhood]] <math>U</math> of <math>x</math>, such that <math>p^{-1}(U)</math> (the [[Image_(mathematics)#Inverse_image|pre-image]] of <math>U</math> under {{nowrap|<math>p</math>)}} is a union of disjoint [[open set]]s in {{nowrap|<math>C</math>,}} each of which is mapped [[homeomorphism|homeomorphically]] onto <math>U</math> by <math>p</math>.<ref name="Chernavskii">{{harvnb|Chernavskii|2001}}</ref><ref name="Munkres p336">{{harvnb|Munkres|2000|p=336}}</ref> |
|||
=== Local homeomorphism === |
|||
Equivalently, a covering space of <math>X</math> may be defined as a [[fiber bundle]] <math>p \colon C \to X</math> with discrete fibers. |
|||
Since a covering <math>\pi:E \rightarrow X</math> maps each of the disjoint open sets of <math>\pi^{-1}(U)</math> homeomorphically onto <math>U</math> it is a local homeomorphism, i.e. <math>\pi</math> is a continuous map and for every <math>e \in E</math> there exists an open neighborhood <math>V \subset E</math> of <math>e</math>, s.t. <math>\pi|_V : V \rightarrow \pi(V)</math> is a homeomorphism. |
|||
It follows that the covering space <math>E</math> and the base space <math>X</math> locally share the same properties. |
|||
The map <math>p</math> is called the '''covering map''',<ref name="Munkres p336"/> the space <math>X</math> is often called the '''base space''' of the covering, and the space <math>C</math> is called the '''total space''' of the covering. For any point <math>x</math> in the base the inverse image of <math>x</math> in <math>C</math> is necessarily a [[discrete space]]<ref name="Munkres p336"/> called the [[Fiber (mathematics)|fiber]] over {{nowrap|<math>x</math>.}} |
|||
* If <math>X</math> is a connected and [[non-orientable manifold]], then there is a covering <math>\pi:\tilde X \rightarrow X</math> of degree <math>2</math>, whereby <math>\tilde X</math> is a connected and orientable manifold.<ref name="Hatcher" /><math>\,^{p.234}</math> |
|||
The special open neighborhoods <math>U</math> of <math>x</math> given in the definition are called '''evenly covered neighborhoods'''. The evenly covered neighborhoods form an [[open cover]] of the space <math>X</math>. The homeomorphic copies in <math>C</math> of an evenly covered neighborhood <math>U</math> are called the '''sheets''' over <math>U</math>. One generally pictures <math>C</math> as "hovering above" <math>X</math>, with <math>p</math> mapping "downwards", the sheets over <math>U</math> being horizontally stacked above each other and above <math>U</math>, and the fiber over <math>x</math> consisting of those points of <math>C</math> that lie "vertically above" {{nowrap|<math>x</math>.}} In particular, covering maps are locally trivial. This means that locally, each covering map is 'isomorphic' to a projection in the sense that there is a homeomorphism, {{nowrap|<math>h</math>,}} from the pre-image {{nowrap|<math>p^{-1}(U)</math>,}} of an evenly covered neighborhood {{nowrap|<math>U</math>,}} onto {{nowrap|<math>U \times F</math>,}} where <math>F</math> is the fiber, satisfying the '''local trivialization condition''', which states the following: if {{nowrap|<math>\pi\colon U \times F \to U</math>}} is the projection onto the first factor, then the composition <math>\pi\circ h: p^{-1}(U) \to U</math> equals <math>p</math> locally (within {{nowrap|<math>p^{-1}(U)</math>).}} |
|||
* If <math>X</math> is a connected [[Lie group]], then there is a covering <math>\pi:\tilde X \rightarrow X</math> which is also a [[Lie group homomorphism]] and <math>\tilde X := \{\gamma:\gamma \text{ is a path in X with }\gamma(0)= \boldsymbol{1_X} \text{ modulo homotopy with fixed ends}\}</math> is a Lie group.<ref>{{Cite book|last=Kühnel |first=Wolfgang |title=Matrizen und Lie-Gruppen|publisher=Springer Fachmedien Wiesbaden GmbH|location=Stuttgart|ISBN=978-3-8348-9905-7}}</ref> <math>^{p.174}</math> |
|||
* If <math>X</math> is a [[Graph theory#Graph|graph]], then it follows for a covering <math>\pi:E \rightarrow X</math> that <math>E</math> is also a graph.<ref name="Hatcher" /> <math>^{p.85}</math> |
|||
* If <math>X</math> is a connected [[manifold]], then there is a covering <math>\pi:\tilde X \rightarrow X</math>, whereby <math>\tilde X</math> is a connected and [[Simply connected space|simply connected]] manifold.<ref name=":0" /> <math>^{p.32}</math> |
|||
* If <math>X</math> is a connected [[Riemann surface]], then there is a covering <math>\pi:\tilde X \rightarrow X</math> which is also a holomorphic map<ref name=":0" /> <math>^{p.22}</math> and <math>\tilde X</math> is a connected and simply connected Riemann surface.<ref name=":0" /> <math>^{p.32}</math> |
|||
=== |
=== Factorisation === |
||
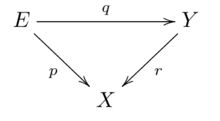
Let <math>p,q</math> and <math>r</math> be continuous maps, s.t. the diagram |
|||
Many authors impose some [[connectedness|connectivity]] conditions on the spaces <math>X</math> and <math>C</math> in the definition of a covering map. In particular, many authors require both spaces to be [[path-connected]] and [[locally path-connected]].<ref>{{Cite book|title = An Introduction to Knot Theory|date = 1997|last = Lickorish|pages = 66–67}}</ref><ref>{{Cite book|title = Topology and Geometry|last = Bredon|first=Glen|author-link=Glen Bredon|year = 1997|isbn = 978-0387979267}}</ref> This can prove helpful because many theorems hold only if the spaces in question have these properties. Some authors omit the assumption of surjectivity, for if <math>X</math> is connected and <math>C</math> is nonempty then surjectivity of the covering map actually follows from the other axioms. |
|||
[[File:Commutativ coverings.png|center|frameless]] |
|||
commutes. |
|||
* If <math>p</math> and <math>q</math> are coverings, so is <math>r</math>.<ref name=":1" /> <math>^{p.485}</math> |
|||
== Examples == |
|||
* If <math>p</math> and <math>r</math> are coverings, so is <math>q</math>.<ref name=":1" /> <math>^{p.485}</math> |
|||
* Every space trivially covers itself. |
|||
* A connected and locally path-connected topological space <math>X</math> has a [[universal cover]] if and only if it is [[semi-locally simply connected]]. |
|||
* <math>\mathbb{R}</math> is the universal cover of the circle <math>S^1.</math> |
|||
* The [[spin group]] <math>\operatorname{Spin}(n)</math> is a double cover of the [[special orthogonal group]] and a universal cover when <math>n > 2</math>. The accidental, or [[exceptional isomorphism]]s for Lie groups then give isomorphisms between spin groups in low dimension and classical Lie groups. |
|||
* The [[unitary group]] <math>\operatorname{U}(n)</math> has universal cover <math>\operatorname{SU}(n)\times\mathbb{R}</math>. |
|||
* The [[n-sphere]] <math>S^n</math> is a double cover of real projective space <math>P_n(\mathbb{R})</math> and is a universal cover for <math>n> 1</math>. |
|||
* Every manifold has an [[orientable double cover]] that is connected if and only if the manifold is non-orientable. |
|||
* The [[uniformization theorem]] asserts that every Riemann surface has a universal cover conformally equivalent to the [[Riemann sphere]], the complex plane, or the unit disc. |
|||
* The universal cover of a wedge of <math>n</math> circles is the [[Cayley graph]] of the free group on <math>n</math> generators, i.e. a [[Bethe lattice]]. |
|||
* The [[torus]] is a double cover of the [[Klein bottle]]. This can be seen using the polygons for the torus and the Klein bottle, and observing that the double cover of the circle <math>S^1 \to S^1</math> (embedding into <math>\mathbb{C}</math> sending <math>z \mapsto z^2</math>). |
|||
* Every graph has a [[bipartite double cover]]. Since every graph is homotopic to a wedge of circles, its universal cover is a Cayley graph. |
|||
* Every immersion from a compact manifold to a manifold of the same dimension is a covering of its image. |
|||
* Another effective tool for constructing covering spaces is using quotients by free finite group actions. |
|||
* For example, the space <math>L_{p/q}</math> is defined by the quotient of <math>S^3</math> (embedded into <math>\mathbb{C}^2</math>) via the <math>\mathbb{Z}/q</math>-action <math>(z_1,z_2) \mapsto (e^{2\pi i/q}z_1,e^{2\pi i p/q}z_2)</math>. This space, called a [[lens space]], has fundamental group <math>\mathbb{Z}/q</math> and has universal cover <math>S^3</math>. |
|||
* The map of [[Spectrum of a ring|affine schemes]] <math>\operatorname{Spec}( \mathbb{C}[x,t,t^{-1}]/(x^n - t)) \to \operatorname{Spec}(\mathbb{C}[t,t^{-1}])</math> forms a covering space with <math>\mathbb{Z}/n</math> as its group of deck transformations. This is an example of a cyclic [[Étale fundamental group|Galois cover]]. |
|||
=== Product of coverings === |
|||
== Properties == |
|||
Let <math>X</math> and <math>X'</math> be topological spaces and <math>p:E \rightarrow X</math> and <math>p':E' \rightarrow X'</math> be coverings, then <math>p \times p':E \times E' \rightarrow X \times X'</math> with <math>(p \times p')(e, e') = (p(e), p'(e'))</math> is a covering.<ref name=":1">{{Cite book|last=Munkres|first=James|title=Topology|publisher=Upper Saddle River, NJ: Prentice Hall, Inc.|year=2000|isbn=978-0-13-468951-7}}</ref> <math>^{p.339}</math> |
|||
=== Equivalence of coverings === |
|||
Let <math>X</math> be a topological space and <math>p:E \rightarrow X</math> and <math>p':E' \rightarrow X</math> be coverings. Both coverings are called '''equivalent''', if there exists a homeomorphism <math>h:E \rightarrow E'</math>, s.t. the diagram |
|||
[[File:Kommutatives_Diagramm_Äquivalenz_von_Überlagerungen.png|center|frameless]] |
|||
commutes. If such a homeomorphism exists, then one calls the covering spaces <math>E</math> and <math>E'</math> [[Isomorphism|isomorphic]]. |
|||
=== Lifting property === |
|||
An important property of the covering is, that it satisfies the [[lifting property]], i.e.: |
|||
Let <math>I</math> be the [[unit interval]] and <math>p:E \rightarrow X</math> be a covering. Let <math>F:Y \times I \rightarrow X</math> be a continuous map and <math>\tilde F_0:Y \times \{0\} \rightarrow E</math> be a lift of <math>F|_{Y \times \{0\}}</math>, i.e. a continuous map such that <math>p \circ \tilde F_0 = F|_{Y \times \{0\}}</math>. Then there is a uniquely determined, continuous map <math>\tilde F:Y \times I \rightarrow E</math>, which is a lift of <math>F</math>, i.e. <math>p \circ \tilde F = F</math>.<ref name="Hatcher" /> <math>^{p.60}</math> |
|||
If <math>X</math> is a path-connected space, then for <math>Y=\{0\}</math> it follows that the map <math>\tilde F</math> is a lift of a [[Path (topology)|path]] in <math>X</math> and for <math>Y=I</math> it is a lift of a [[homotopy]] of paths in <math>X</math>. |
|||
Because of that property one can show, that the [[fundamental group]] <math>\pi_{1}(S^1)</math> of the unit circle is an [[Cyclic group|infinite cyclic group]], which is generated by the homotopy classes of the loop <math>\gamma: I \rightarrow S^1</math> with <math>\gamma (t) = (\cos(2 \pi t), \sin(2 \pi t))</math>.<ref name="Hatcher" /> <math>^{p.29}</math> |
|||
Let <math>X</math> be a path-connected space and <math>p:E \rightarrow X</math> be a connected covering. Let <math>x,y \in X</math> be any two points, which are connected by a path <math>\gamma</math>, i.e. <math>\gamma(0)= x</math> and <math>\gamma(1)= y</math>. Let <math>\tilde \gamma</math> be the unique lift of <math>\gamma</math>, then the map |
|||
: <math>L_{\gamma}:p^{-1}(x) \rightarrow p^{-1}(y)</math> with <math>L_{\gamma}(\tilde \gamma (0))=\tilde \gamma (1)</math> |
|||
is [[Bijection|bijective]].<ref name="Hatcher" /> <math>^{p.69 }</math> |
|||
If <math>X</math> is a path-connected space and <math>p: E \rightarrow X</math> a connected covering, then the induced [[group homomorphism]] |
|||
: <math> p_{\#}: \pi_{1}(E) \rightarrow \pi_{1}(X)</math> with <math> p_{\#}([\gamma])=[p \circ \gamma]</math>, |
|||
is [[Injective function|injective]] and the [[subgroup]] <math>p_{\#}(\pi_1(E))</math> of <math>\pi_1(X)</math> consists of the homotopy classes of loops in <math>X</math>, whose lifts are loops in <math>E</math>.<ref name="Hatcher" /> <math>^{p.61}</math> |
|||
== Branched covering == |
|||
=== Definitions === |
|||
==== Holomorphic maps between Riemann surfaces ==== |
|||
Let <math>X</math> and <math>Y</math> be [[Riemann surface|Riemann surfaces]], i.e. one dimensional [[Complex manifold|complex manifolds]], and let <math>f: X \rightarrow Y</math> be a continuous map. <math>f</math> is '''holomorphic in a point''' <math>x \in X</math>, if for any [[Chart (mathematics)|charts]] <math>\phi _x:U_1 \rightarrow V_1</math> of <math>x</math> and <math>\phi_{f(x)}:U_2 \rightarrow V_2</math> of <math>f(x)</math>, with <math>\phi_x(U_1) \subset U_2</math>, the map <math>\phi _{f(x)} \circ f \circ \phi^{-1} _x: \mathbb{C} \rightarrow \mathbb{C}</math> is [[Holomorphic function|holomorphic]]. |
|||
If <math>f</math> is for all <math>x \in X</math> holomorphic, we say <math>f</math> is '''holomorphic.''' |
|||
The map <math>F =\phi _{f(x)} \circ f \circ \phi^{-1} _x</math> is called the '''local expression''' of <math>f</math> in <math>x \in X</math>. |
|||
If <math>f: X \rightarrow Y</math> is a non-constant, holomorphic map between [[Compact riemann surface|compact Riemann surfaces]], then <math>f</math> is [[Surjective function|surjective]]<ref name=":0">{{Cite book|last=Forster|first=Otto|title=Lectures on Riemann surfaces|publisher=Springer Berlin|year=1991|isbn=978-3-540-90617-9|location=München|pages=}}</ref> <math>^{p.11}</math> and an [[open map]]<ref name=":0" /> <math>^{p.11}</math>, i.e. for every open set <math>U \subset X</math> the [[Image (mathematics)|image]] <math>f(U) \subset Y</math> is also open. |
|||
==== Ramification point and branch point ==== |
|||
Let <math>f: X \rightarrow Y</math> be a non-constant, holomorphic map between compact Riemann surfaces. For every <math>x \in X</math> there exist charts for <math>x</math> and <math>f(x)</math> and there exists a uniquely determined <math>k_x \in \mathbb{N_{>0}}</math>, s.t. the local expression <math>F</math> of <math>f</math> in <math>x</math> is of the form <math>z \mapsto z^{k_{x}}</math>.<ref name=":0" /> <math>^{p.10 }</math> The number <math>k_x</math> is called the '''ramification index''' of <math>f</math> in <math>x</math> and the point <math>x \in X</math> is called a '''ramification point''' if <math>k_x \geq 2</math>. If <math>k_x =1</math> for an <math>x \in X</math>, then <math>x</math> is '''unramified'''. The image point <math>y=f(x) \in Y</math> of a ramification point is called a '''branch point.''' |
|||
==== Degree of a holomorphic map ==== |
|||
===Common local properties=== |
|||
Let <math>f: X \rightarrow Y</math> be a non-constant, holomorphic map between compact Riemann surfaces. The '''degree <math>deg(f)</math>''' of <math>f</math> is the cardinality of the fiber of an unramified point <math>y=f(x) \in Y</math>, i.e. <math>deg(f):=|f^{-1}(y)|</math>. |
|||
* Every cover <math> p \colon C \to X </math> is a [[local homeomorphism]];<ref>{{harvnb|Munkres|2000|p=338}}</ref> that is, for every <math>c\in C</math>, there exists a neighborhood <math>U\subseteq C</math> of ''c'' and a neighborhood <math>V\subseteq X</math> of <math>p(c)</math> such that the restriction of ''p'' to ''U'' yields a [[homeomorphism]] from ''U'' to ''V''. This implies that ''C'' and ''X'' share all local properties. If ''X'' is [[simply connected]] and ''C'' is connected, then this holds globally as well, and the covering ''p'' is a homeomorphism. |
|||
* If <math>p\colon E\to B</math> and <math>p'\colon E'\to B'</math> are covering maps, then so is the map <math>p \times p' \colon E\times E' \to B\times B'</math> given by <math>(p\times p')(e, e') = (p(e), p'(e'))</math>.<ref>{{harvnb|Munkres|2000|p=339|loc=Theorem 53.3}}</ref> |
|||
This number is well-defined, since for every <math>y \in Y</math> the fiber <math>f^{-1}(y)</math> is discrete<ref name=":0" /> <math>^{p.20}</math> and for any two unramified points <math>y_1,y_2 \in Y</math>, it is: <math>|f^{-1}(y_1)|=|f^{-1}(y_2)|.</math><ref name=":0" /> <math>^{p.29}</math> |
|||
===Homeomorphism of the fibers=== |
|||
For every ''x'' in ''X'', the fiber over ''x'' is a [[discrete space|discrete]] subset of ''C''.<ref name="Munkres p336"/> On every [[connected space|connected component]] of ''X'', the fibers are homeomorphic. |
|||
It can be calculated by: |
|||
If ''X'' is connected, there is a discrete space ''F'' such that for every ''x'' in ''X'' the fiber over ''x'' is [[homeomorphism|homeomorphic]] to ''F'' and, moreover, for every ''x'' in ''X'' there is a neighborhood ''U'' of ''x'' such that its full pre-image ''p''<sup>−1</sup>(''U'') is homeomorphic to {{nowrap|''U'' × ''F''}}. In particular, the [[cardinality]] of the fiber over ''x'' is equal to the cardinality of ''F'' and it is called the '''degree of the cover''' {{nowrap|''p'' : ''C'' → ''X''}}. Thus, if every fiber has ''n'' elements, we speak of an '''''n''-fold covering''' (for the case {{nowrap|1=''n'' = 1}}, the covering is trivial; when {{nowrap|1=''n'' = 2}}, the covering is a '''double cover'''; when {{nowrap|1=''n'' = 3}}, the covering is a '''triple cover''' and so on). |
|||
: <math>\sum_{x \in f^{-1}(y)} k_x = deg(f)</math> <ref name=":0" /> <math>^{p.29}</math> |
|||
===Lifting properties=== |
|||
{{see also|Homotopy lifting property}} |
|||
If {{nowrap|1=''p'' : ''C'' → ''X''}} is a cover and γ is a path in ''X'' (i.e. a continuous map from the [[unit interval]] {{nowrap|[0, 1]}} into ''X'') and {{nowrap|''c'' ∈ ''C''}} is a point "lying over" γ(0) (i.e. {{nowrap|1=''p''(''c'') = γ(0))}}, then there exists a unique path Γ in ''C'' lying over γ (i.e. {{nowrap|1=''p'' ∘ Γ = γ}}) such that {{nowrap|1=Γ(0) = ''c''}}. The curve Γ is called the '''lift''' of γ. If ''x'' and ''y'' are two points in ''X'' connected by a path, then that path furnishes a [[bijection]] between the fiber over ''x'' and the fiber over ''y'' via the lifting property. |
|||
=== Branched covering === |
|||
More generally, let {{nowrap|''f'' : ''Z'' → ''X''}} be a continuous map to ''X'' from a [[path connected]] and [[locally path connected]] space ''Z''. Fix a base-point {{nowrap|''z'' ∈ ''Z''}}, and choose a point {{nowrap|''c'' ∈ ''C''}} "lying over" ''f''(''z'') (i.e. {{nowrap|1=''p''(''c'') = ''f''(''z'')}}). Then there exists a '''lift''' of ''f'' (that is, a continuous map {{nowrap|''g'' : ''Z'' → ''C''}} for which {{nowrap|1=''p'' ∘ ''g'' = ''f''}} and {{nowrap|1=''g''(''z'') = ''c''}}) [[if and only if]] the [[induced homomorphism]]s {{nowrap|''f''<sub>#</sub> : {{pi}}<sub>1</sub>(''Z'', ''z'') → {{pi}}<sub>1</sub>(''X'', ''f''(''z''))}} and {{nowrap|''p''<sub>#</sub> : {{pi}}<sub>1</sub>(''C'', ''c'') → {{pi}}<sub>1</sub>(''X'', ''f''(''z''))}} at the level of [[fundamental groups]] satisfy |
|||
{{NumBlk||<math display="block">f_\#(\pi_1(Z,z))\subset p_\#(\pi_1(C,c)). </math>|{{EquationRef|♠}}}} |
|||
==== Definition ==== |
|||
Moreover, if such a lift ''g'' of ''f'' exists, it is unique. |
|||
A continuous map <math>f: X \rightarrow Y</math> is called a '''branched covering''', if there exists a [[closed set]] with [[Dense set|dense]] complement <math>E \subset Y</math>, s.t. <math>f_{|X \smallsetminus f^{-1}(E)}:X \smallsetminus f^{-1}(E) \rightarrow Y \smallsetminus E</math> is a covering. |
|||
==== Examples ==== |
|||
In particular, if the space ''Z'' is assumed to be [[simply connected]] (so that {{nowrap|{{pi}}<sub>1</sub>(''Z'', ''z'')}} is trivial), condition {{EquationNote|♠|(♠)}} is automatically satisfied, and every continuous map from ''Z'' to ''X'' can be lifted. Since the unit interval {{nowrap|[0, 1]}} is simply connected, the lifting property for paths is a special case of the lifting property for maps stated above. |
|||
* Let <math>n \in \mathbb{N}</math> and <math>n \geq 2</math>, then <math>f:\mathbb{C} \rightarrow \mathbb{C}</math> with <math>f(z)=z^n</math> is branched covering of degree <math>n</math>, whereby <math>z=0</math> is a branch point. |
|||
If {{nowrap|''p'' : ''C'' → ''X''}} is a covering and {{nowrap|''c'' ∈ ''C''}} and {{nowrap|''x'' ∈ ''X''}} are such that {{nowrap|1=''p''(''c'') = ''x''}}, then ''p''<sub>#</sub> is injective at the level of [[fundamental groups]], and the induced homomorphisms {{nowrap|''p''<sub>#</sub> : {{pi}}<sub>''n''</sub>(''C'', ''c'') → {{pi}}<sub>''n''</sub>(''X'', ''x'')}} are [[group isomorphism|isomorphisms]] for all {{nowrap|''n'' ≥ 2}}. Both of these statements can be deduced from the lifting property for continuous maps. Surjectivity of ''p''<sub>#</sub> for {{nowrap|''n'' ≥ 2}} follows from the fact that for all such ''n'', the ''n''-sphere '''S'''<sup>''n''</sup> is simply connected and hence every continuous map from '''S'''<sup>''n''</sup> to ''X'' can be lifted to ''C''. |
|||
* Every non-constant, holomorphic map between compact Riemann surfaces <math>f: X \rightarrow Y</math> of degree <math>d</math> is a branched covering of degree <math>d</math>. |
|||
== Universal covering == |
|||
===Equivalence=== |
|||
Let <math>p: \tilde X \rightarrow X</math> be a [[Simply connected space|simply connected]] covering and <math>\beta : E \rightarrow X</math> be a covering, then there exists a uniquely determined covering <math>\alpha : \tilde X \rightarrow E</math>, s.t. the diagram |
|||
Let {{nowrap|''p''<sub>1</sub> : ''C''<sub>1</sub> → ''X''}} and {{nowrap|''p''<sub>2</sub> : ''C''<sub>2</sub> → ''X''}} be two coverings. One says that the two coverings ''p''<sub>1</sub> and ''p''<sub>2</sub> are '''equivalent''' if there exists a homeomorphism {{nowrap|''p''<sub>21</sub> : ''C''<sub>2</sub> → ''C''<sub>1</sub>}} and such that {{nowrap|1=''p''<sub>2</sub> = ''p''<sub>1</sub> ∘ ''p''<sub>21</sub>}}. Equivalence classes of coverings correspond to conjugacy classes of subgroups of the [[fundamental group]] of ''X'', as discussed below. If {{nowrap|''p''<sub>21</sub> : ''C''<sub>2</sub> → ''C''<sub>1</sub>}} is a covering (rather than a homeomorphism) and {{nowrap|1=''p''<sub>2</sub> = ''p''<sub>1</sub> ∘ ''p''<sub>21</sub>}}, then one says that ''p''<sub>2</sub> '''dominates''' ''p''<sub>1</sub>. |
|||
[[File:Universelle Überlagerung 2.0.png|center|frameless]] |
|||
commutes.<ref name=":1" /> <math>^{p.486 }</math> |
|||
===Covering of a manifold=== |
|||
Since coverings are local [[homeomorphism]]s, a covering of a topological ''n''-[[manifold]] is an ''n''-manifold. (One can prove that the covering space is [[second-countable]] from the fact that the [[fundamental group]] of a manifold is always [[countable]].) However a space covered by an ''n''-manifold may be a [[non-Hausdorff manifold]]. An example is given by letting ''C'' be the plane with the origin deleted and ''X'' the quotient space obtained by identifying every point {{nowrap|(''x'', ''y'')}} with {{nowrap|(2''x'', ''y''/2)}}. If {{nowrap|''p'' : ''C'' → ''X''}} is the quotient map then it is a covering since the action of ''Z'' on ''C'' generated by {{nowrap|1=''f''(''x'', ''y'') = (2''x'', ''y''/2)}} is free and wandering (but not [[properly discontinuous]]). The points {{nowrap|''p''(1, 0)}} and {{nowrap|''p''(0, 1)}} do not have disjoint neighborhoods in ''X''. |
|||
=== Definition === |
|||
Any covering space of a differentiable manifold may be equipped with a (natural) differentiable structure that turns ''p'' (the covering map in question) into a [[local diffeomorphism]] – a map with constant [[Rank (differential topology)|rank]] ''n''. |
|||
Let <math>p: \tilde X \rightarrow X</math> be a simply connected covering. If <math>\beta : E \rightarrow X</math> is another simply connected covering, then there exists a uniquely determined homeomorphism <math>\alpha : \tilde X \rightarrow E</math>, s.t. the diagram |
|||
[[File:Universelle_Überlagerung_2.0.png|center|frameless]] |
|||
commutes.<ref name=":1" /> <math>^{p.482}</math> |
|||
This means that <math>p</math> is, up to equivalence, uniquely determined and because of that [[universal property]] denoted as the '''universal covering''' of the space <math>X</math>. |
|||
== Universal covers == |
|||
{{Redirect2|Universal cover|Universal covering|the Kakeya-type problem|Lebesgue's universal covering problem}} |
|||
A covering space is a '''universal covering space''' if it is [[simply connected]]. The name ''[[universal property|universal]] cover'' comes from the following important property: if the mapping {{nowrap|''q'': ''D'' → ''X''}} is a universal cover of the space ''X'' and the mapping {{nowrap|''p'' : ''C'' → ''X''}} is any cover of the space ''X'' where the covering space ''C'' is connected, then there exists a covering map {{nowrap|''f'' : ''D'' → ''C''}} such that {{nowrap|1=''p'' ∘ ''f'' = ''q''}}. This can be phrased as |
|||
=== Existence === |
|||
<blockquote>The universal cover (of the space ''X'') covers any connected cover (of the space ''X'').</blockquote> |
|||
A universal covering does not always exists, but the following properties guarantee the existence: |
|||
Let <math>X</math> be a connected, [[Locally simply connected space|locally simply connected]], then there exists a universal covering <math>p:\tilde X \rightarrow X</math>. |
|||
The map ''f'' is unique in the following sense: if we fix a point ''x'' in the space ''X'' and a point ''d'' in the space ''D'' with {{nowrap|1=''q''(''d'') = ''x''}} and a point ''c'' in the space ''C'' with {{nowrap|1=''p''(''c'') = ''x''}}, then there exists a unique covering map {{nowrap|''f'' : ''D'' → ''C''}} such that {{nowrap|1=''p'' ∘ ''f'' = ''q''}} and {{nowrap|1=''f''(''d'') = ''c''}}. |
|||
<math>\tilde X</math> is defined as <math>\tilde X := \{\gamma:\gamma \text{ is a path in }X \text{ with }\gamma(0) = x_0 \}/\text{ homotopy with fixed ends} </math> and <math>p:\tilde X \rightarrow X</math> by <math>p([\gamma]):=\gamma(1)</math>.<ref name="Hatcher" /> <math>^{p.64}</math> |
|||
If the space ''X'' has a universal cover then that universal cover is essentially unique: if the mappings {{nowrap|''q''<sub>1</sub> : ''D''<sub>1</sub> → ''X''}} and {{nowrap|''q''<sub>2</sub> : ''D''<sub>2</sub> → ''X''}} are two universal covers of the space ''X'' then there exists a homeomorphism {{nowrap|''f'' : ''D''<sub>1</sub> → ''D''<sub>2</sub>}} such that {{nowrap|1=''q''<sub>2</sub> ∘ ''f'' = ''q''<sub>1</sub>}}. |
|||
The [[topology]] on <math>\tilde X</math> is constructed as follows: Let <math>\gamma:I \rightarrow X</math> be a path with <math>\gamma(0)=x_0</math>. Let <math>U</math> be a simply connected neighborhood of the endpoint <math>x=\gamma(1)</math>, then for every <math>y \in U</math> the [[Path (topology)|paths]] <math>\sigma_y</math> inside <math>U </math> from <math>x</math> to <math>y</math> are uniquely determined up to [[homotopy]]. Now consider <math>\tilde U:=\{\gamma.\sigma_y:y \in U \}/\text{ homotopy with fixed ends}</math>, then <math>p_{|\tilde U}: \tilde U \rightarrow U</math> with <math>p([\gamma.\sigma_y])=\gamma.\sigma_y(1)=y</math> is a bijection and <math>\tilde U</math> can be equipped with the [[final topology]] of <math>p_{|\tilde U}</math>. |
|||
The space ''X'' has a universal cover if it is [[Connected space|connected]], [[Connected space#Local connectedness|locally path-connected]] and [[semi-locally simply connected]]. The universal cover of the space ''X'' can be constructed as a certain space of paths in the space ''X''. More explicitly, it forms a [[principal bundle]] with the [[fundamental group]] {{math|''π''<sub>1</sub>(''X'')}} as structure group. |
|||
The fundamental group <math>\pi_{1}(X,x_0) = \Gamma</math> acts [[Free group action|freely]] through <math>([\gamma],[\tilde x]) \mapsto [\gamma.\tilde x]</math> on <math>\tilde X</math> and <math>\psi:\Gamma \backslash \tilde X \rightarrow X</math> with <math>\psi([\Gamma \tilde x])=\tilde x(1)</math> is a homeomorphism, i.e. <math>\Gamma \backslash \tilde X \cong X </math>. |
|||
The example {{nowrap|'''R''' → '''S'''<sup>1</sup>}} given above is a universal cover. The map {{nowrap|'''S'''<sup>3</sup> → SO(3)}} from [[quaternion|unit quaternions]] to [[rotation]]s of 3D space described in [[quaternions and spatial rotation]] is also a universal cover. |
|||
=== Examples === |
|||
If the space <math>X</math> carries some additional structure, then its universal cover usually inherits that structure: |
|||
* If the space <math>X</math> is a [[manifold]], then so is its universal cover ''D''. |
|||
* If the space <math>X</math> is a [[Riemann surface]], then so is its universal cover ''D'', and <math>p</math> is a [[Holomorphic function|holomorphic]] map. |
|||
* If the space <math>X</math> is a [[Riemannian manifold]], then so is its universal cover, and <math>p</math> is a [[Isometry (Riemannian geometry)|local isometry]]. |
|||
* If the space <math>X</math> is a [[Lorentzian manifold]], then so is its universal cover. Furthermore, suppose the subset ''p''<sup>−1</sup>(''U'') is a [[disjoint union]] of open sets each of which is diffeomorphic with ''U'' by the mapping <math>p</math>. If the space <math>X</math> contains a [[closed timelike curve]] (CTC), then the space <math>X</math> is [[timelike multiply connected]] (no CTC can be [[timelike homotopic]] to a point, as that point would not be causally well behaved), its universal (diffeomorphic) cover is [[timelike simply connected]] (it does not contain a CTC). |
|||
* If ''X'' is a [[Lie group]] (as in the two examples above), then so is its universal cover ''D'', and the mapping ''p'' is a homomorphism of Lie groups. In this case the universal cover is also called the ''[[universal covering group]]''. This has particular application to [[representation theory]] and [[quantum mechanics]], since ordinary [[Group representation|representations]] of the universal covering group (''D'') are [[projective representation]]s of the original (classical) group (''X''). |
|||
* <math>r \colon \mathbb{R} \to S^1</math> with <math>r(t)=(\cos(2 \pi t), \sin(2 \pi t))</math> is the universal covering of the unit circle <math>S^1</math>. |
|||
The universal cover first arose in the theory of [[analytic functions]] as the natural domain of an [[analytic continuation]]. |
|||
* <math>p \colon S^n \to \mathbb{R}P^n \cong \{+1,-1\}\backslash S^n</math> with <math>p(x)=[x]</math> is the universal covering of the [[projective space]] <math>\mathbb{R}P^n</math> for <math>n>1</math>. |
|||
* <math>q \colon SU(n) \ltimes \mathbb{R} \to U(n)</math> with <math>q(A,t)= \begin{bmatrix} |
|||
\exp(2 \pi i t) & 0\\ |
|||
0 & I_{n-1} |
|||
\end{bmatrix} A</math> is the universal covering of the [[unitary group]] <math>U(n)</math>.<ref>{{Cite journal|last=Aguilar|first=Maximiliano|last2=Socolovsky|first2=Miguel|date=December 1999|title=The Universal Covering Group of U(n) and Projective Representations|journal=International Journal of Theoretical Physics|pages=5 Theorem 1}}</ref> |
|||
* Since <math>SU(2) \cong S^3</math>, it follows that the [[quotient map]] <math>f:SU(2) \rightarrow \mathbb{Z_2} \backslash SU(2) \cong SO(3)</math> is the universal covering of the <math>SO(3)</math>.[[File:Hawaiian_Earrings.svg|right|thumb|250x250px|The Hawaiian earring. Only the ten largest circles are shown.]] |
|||
* A topological space, which has no universal covering is the [[Hawaiian earring]]: |
|||
: <math>X=\bigcup_{n\in \N}\left\{(x_1,x_2)\in\R^{2} : \Bigl(x_1-\frac{1}{n}\Bigr)^2+x_2^2=\frac{1}{n^2}\right\}</math> |
|||
== G-coverings == |
|||
: One can show, that no neighborhood of the origin <math>(0,0)</math> is simply connected.<ref name=":1" /> <math>^{p.487 \, Example \, 1 }</math> |
|||
Let ''G'' be a [[discrete group]] [[Group action (mathematics)|acting]] on the [[topological space]] ''X''. This means that each element ''g'' of ''G'' is associated to a homeomorphism H<sub>''g''</sub> of ''X'' onto itself, in such a way that H<sub>''g'' ''h''</sub> is always equal to H<sub>''g''</sub> ∘ H<sub>''h''</sub> for any two elements ''g'' and ''h'' of ''G''. (Or in other words, a group action of the group ''G'' on the space ''X'' is just a group homomorphism of the group ''G'' into the group Homeo(''X'') of self-homeomorphisms of ''X''.) It is natural to ask under what conditions the projection from ''X'' to the [[orbit space]] ''X''/''G'' is a covering map. This is not always true since the action may have fixed points. An example for this is the cyclic group of order 2 acting on a product {{nowrap|''X'' × ''X''}} by the twist action where the non-identity element acts by {{nowrap|(''x'', ''y'') ↦ (''y'', ''x'')}}. Thus the study of the relation between the fundamental groups of ''X'' and ''X''/''G'' is not so straightforward. |
|||
== Deck transformation == |
|||
However the group ''G'' does act on the fundamental groupoid of ''X'', and so the study is best handled by considering groups acting on groupoids, and the corresponding ''orbit groupoids''. The theory for this is set down in Chapter 11 of the book ''Topology and groupoids'' referred to below. The main result is that for discontinuous actions of a group ''G'' on a Hausdorff space ''X'' which admits a universal cover, then the fundamental groupoid of the orbit space ''X''/''G'' is isomorphic to the orbit groupoid of the fundamental groupoid of ''X'', i.e. the quotient of that groupoid by the action of the group ''G''. This leads to explicit computations, for example of the fundamental group of the symmetric square of a space. |
|||
=== Definition === |
|||
== {{anchor|Deck transformation}} Deck (covering) transformation group, regular covers == |
|||
Let <math>p:E \rightarrow X</math> be a covering. A '''deck transformation''' is a homeomorphism <math>d:E \rightarrow E</math>, s.t. the diagram of continuous maps |
|||
A '''covering transformation''' or '''deck transformation''' or '''automorphism''' of a cover <math>p:C \to X</math> is a [[homeomorphism]] <math>f:C \to C</math> such that <math>p \circ f = p </math>. The set of all deck transformations of <math>p</math> forms a group under [[function composition|composition]], the '''deck transformation group''' <math>\operatorname{Aut}(p)</math>. Deck transformations are also called '''covering transformations'''. Every deck transformation [[permutation|permutes]] the elements of each fiber. This defines a [[Group action (mathematics)|group action]] of the deck transformation group on each fiber. Note that by the unique lifting property, if <math>f</math> is not the identity and <math>C</math> is path connected, then <math>f</math> has no [[fixed point (mathematics)|fixed points]]. |
|||
[[File:Diagramm_Decktrafo.png|center|frameless]] |
|||
commutes. Together with the composition of maps, the set of deck transformation forms a [[Group (mathematics)|group]] <math>Deck(p)</math>, which is the same as <math>Aut(p)</math>. |
|||
=== Examples === |
|||
Now suppose <math>p:C \to X</math> is a covering map and <math>C</math> (and therefore also <math>X</math>) is connected and locally path connected. The action of <math>\operatorname{Aut}(p)</math> on each fiber is [[Group action (mathematics)#Types of actions|free]]. If this action is [[Group action (mathematics)#Types of actions|transitive]] on some fiber, then it is transitive on all fibers, and we call the cover '''regular''' (or '''normal''' or '''Galois'''). Every such regular cover is a [[principal bundle|principal {{nowrap|<math>G</math>-bundle}}]], where <math>G = \operatorname{Aut}(p)</math> is considered as a discrete topological group. |
|||
* Let <math>q \colon S^1 \to S^1</math> be the covering <math>q(z)=z^{n}</math> for some <math>n \in \mathbb{N} </math>, then the map <math>d:S^1 \rightarrow S^1 : z \mapsto z \, e^{2\pi i/n} </math> is a deck transformation and <math>Deck(q)\cong \mathbb{Z}/ \mathbb{nZ}</math>. |
|||
Every universal cover <math>p:D \to X </math> is regular, with deck transformation group being isomorphic to the [[fundamental group]] {{nowrap|<math>\pi_1(X)</math>.}} |
|||
* Let <math>r \colon \mathbb{R} \to S^1</math> be the covering <math>r(t)=(\cos(2 \pi t), \sin(2 \pi t))</math>, then the map <math>d_k:\mathbb{R} \rightarrow \mathbb{R} : t \mapsto t + k</math> with <math>k \in \mathbb{Z}</math> is a deck transformation and <math>Deck(r)\cong \mathbb{Z}</math>. |
|||
=== Properties === |
|||
As another important example, consider <math>\Complex</math> the complex plane and <math>\Complex^{\times}</math> the complex plane minus the origin. Then the map <math>p\colon \Complex^{\times} \to \Complex^{\times}</math> with <math> p(z) = z^{n} </math> is a regular cover. The deck transformations are multiplications with <math>n</math>-th [[root of unity|roots of unity]] and the deck transformation group is therefore isomorphic to the [[cyclic group]] <math>\Z/n\Z</math>. Likewise, the map <math>\exp\colon \Complex \to \Complex^{\times}</math> with <math>\exp(z) = e^{z}</math> is the universal cover. |
|||
Let <math>X</math> be a path-connected space and <math>p:E \rightarrow X</math> be a connected covering. Since a deck transformation <math>d:E \rightarrow E</math> is [[Bijection|bijective]], it permutes the elements of a fiber <math>p^{-1}(x)</math> with <math>x \in X</math> and is uniquely determined by where it sends a single point. In particular, only the identity map fixes a point in the fiber.<ref name="Hatcher" /> <math>^{p.70 }</math>Because of this property every deck transformation defines a [[group action]] on <math>E</math>, i.e. let <math>U \subset X</math> be an open neighborhood of a <math>x \in X</math> and <math>\tilde U \subset E</math> an open neighborhood of an <math>e \in p^{-1}(x)</math>, then <math>Deck(p) \times E \rightarrow E: (d,\tilde U)\mapsto d(\tilde U)</math> is a [[group action]]. |
|||
== |
=== Normal coverings === |
||
{{main|Monodromy}} |
|||
Again suppose <math>p\colon C\to X</math> is a covering map and ''C'' (and therefore also ''X'') is connected and locally path connected. If ''x'' is in ''X'' and ''c'' belongs to the fiber over ''x'' (i.e., <math>p(c) = x</math>), and <math>\gamma\colon [0, 1] \to X</math> is a path with <math>\gamma(0) = \gamma(1) = x</math>, then this path lifts to a unique path in ''C'' with starting point ''c''. The end point of this lifted path need not be ''c'', but it must lie in the fiber over ''x''. It turns out that this end point only depends on the class of γ in the fundamental group {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}}. In this fashion we obtain a right [[Group action (mathematics)|group action]] of {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}} on the fiber over ''x''. This is known as the '''monodromy action'''. |
|||
==== Definition ==== |
|||
There are two actions on the fiber over {{nowrap|''x'' : Aut(''p'')}} acts on the left and {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}} acts on the right. These two actions are compatible in the following sense: |
|||
A covering <math>p:E \rightarrow X</math> is called normal, if <math>Deck(p) \backslash X \cong E</math>. This means, that for every <math>x \in X</math> and any two <math>e_0,e_1 \in p^{-1}(x)</math> there exists a deck transformation <math>d:E \rightarrow E</math>, s.t. <math>d(e_0)=e_1</math>. |
|||
<math>f\cdot(c\cdot\gamma) = (f\cdot c)\cdot\gamma</math> for all ''f'' in Aut(''p''), ''c'' in ''p''<sup>−1</sup>(''x'') and γ in {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}}. |
|||
==== Properties ==== |
|||
If ''p'' is a universal cover, then Aut(''p'') can be naturally identified with the [[opposite group]] of {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}} so that the left action of the opposite group of {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}} coincides with the action of Aut(''p'') on the fiber over ''x''. Note that Aut(''p'') and {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}} are naturally isomorphic in this case (as a group is always naturally isomorphic to its opposite through {{nowrap|''g'' ↦ ''g''<sup>−1</sup>)}}. |
|||
Let <math>X</math> be a path-connected space and <math>p:E \rightarrow X</math> be a connected covering. Let <math>H=p_{\#}(\pi_1(E))</math> be a [[subgroup]] of <math>\pi_1(X)</math>, then <math>p</math> is a normal covering iff <math>H</math> is a [[normal subgroup]] of <math>\pi_1(X)</math>.<ref name="Hatcher" /> <math>^{p.71}</math> |
|||
If <math>p:E \rightarrow X</math> is a normal covering and <math>H=p_{\#}(\pi_1(E))</math>, then <math>Deck(p) \cong \pi_1(X)/H</math>.<ref name="Hatcher" /> <math>^{p.71}</math> |
|||
If ''p'' is a [[#Deck transformation group.2C regular covers|regular]] cover, then Aut(''p'') is naturally isomorphic to a quotient of {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}}. |
|||
If <math>p:E \rightarrow X</math> is a path-connected covering and <math>H=p_{\#}(\pi_1(E))</math>, then <math>Deck(p) \cong N(H)/H</math>, whereby <math>N(H)</math> is the [[normaliser]] of <math>H</math>.<ref name="Hatcher" /> <math>^{p.71}</math> |
|||
In general (for good spaces), Aut(''p'') is naturally isomorphic to the quotient of the [[Centralizer and normalizer|normalizer]] of {{nowrap|''p''<sub>*</sub>({{pi}}<sub>1</sub>(''C'', ''c''))}} in {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}} over {{nowrap|''p''<sub>*</sub>({{pi}}<sub>1</sub>(''C'', ''c''))}}, where {{nowrap|1=''p''(''c'') = ''x''}}. |
|||
Let <math>E</math> be a topological space. A group <math>\Gamma</math> acts '''discontinuously''' on <math>E</math>, if every <math>e \in E</math> has an open neighborhood <math>V \subset E</math> with <math>V \neq \empty</math>, such that for every <math>\gamma \in \Gamma</math> with <math>\gamma V \cap V \neq \empty</math> one has <math>d_1 = d_2</math>. |
|||
==More on the group structure== |
|||
Let {{nowrap|''p'' : ''C'' → ''X''}} be a covering map where both ''X'' and ''C'' are path-connected. Let {{nowrap|''x'' ∈ ''X''}} be a basepoint of ''X'' and let {{nowrap|''c'' ∈ ''C''}} be one of its pre-images in ''C'', that is {{nowrap|1=''p''(''c'') = ''x''}}. There is an [[induced homomorphism]] of [[fundamental group]]s {{nowrap|''p''<sub>#</sub> : {{pi}}<sub>1</sub>(''C'', ''c'') → {{pi}}<sub>1</sub>(''X'',''x'')}} which is injective by the lifting property of coverings. Specifically if ''γ'' is a closed loop at ''c'' such that {{nowrap|1=''p''<sub>#</sub>([''γ'']) = 1}}, that is {{nowrap|''p'' ∘ ''γ''}} is [[null-homotopic]] in ''X'', then consider a null-homotopy of {{nowrap|''p'' ∘ ''γ''}} as a map {{nowrap|''f'' : ''D''<sup>2</sup> → ''X''}} from the 2-disc ''D''<sup>2</sup> to ''X'' such that the restriction of ''f'' to the boundary '''S'''<sup>1</sup> of ''D''<sup>2</sup> is equal to {{nowrap|''p'' ∘ ''γ''}}. By the lifting property the map ''f'' lifts to a continuous map {{nowrap|''g'' : ''D''<sup>2</sup> → ''C''}} such that the restriction of ''g'' to the boundary '''S'''<sup>1</sup> of ''D''<sup>2</sup> is equal to ''γ''. Therefore, ''γ'' is [[null-homotopic]] in ''C'', so that the [[Kernel (algebra)|kernel]] of {{nowrap|''p''<sub>#</sub> : {{pi}}<sub>1</sub>(''C'', ''c'') → {{pi}}<sub>1</sub>(''X'', ''x'')}} is trivial and thus {{nowrap|''p''<sub>#</sub> : {{pi}}<sub>1</sub>(''C'', ''c'') → {{pi}}<sub>1</sub>(''X'', ''x'')}} is an injective homomorphism. |
|||
If a group <math>\Gamma</math> acts discontinuously on a topological space <math>E</math>, then the [[quotient map]] <math>q: E \rightarrow \Gamma \backslash E </math> with <math>q(e)=\Gamma e</math> is a normal covering.<ref name="Hatcher" /> <math>^{p.72}</math> Hereby <math>\Gamma \backslash E = \{\Gamma e: e \in E\}</math> is the [[Quotient space (topology)|quotient space]] and <math>\Gamma e = \{\gamma(e):\gamma \in \Gamma\}</math> is the [[Orbit (group theory)|orbit]] of the group action. |
|||
Therefore, {{nowrap|{{pi}}<sub>1</sub>(''C'', ''c'')}} is isomorphic to the subgroup {{nowrap|''p''<sub>#</sub>({{pi}}<sub>1</sub>(''C'', ''c''))}} of {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}}. If {{nowrap|''c''<sub>1</sub> ∈ ''C''}} is another pre-image of ''x'' in ''C'' then the [[subgroup]]s {{nowrap|''p''<sub>#</sub>({{pi}}<sub>1</sub>(''C'', ''c''))}} and {{nowrap|''p''<sub>#</sub>({{pi}}<sub>1</sub>(''C'', ''c''<sub>1</sub>))}} are [[conjugacy class|conjugate]] in {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}} by ''p''-image of a curve in ''C'' connecting ''c'' to ''c''<sub>1</sub>. Thus a covering map {{nowrap|''p'' : ''C'' → ''X''}} defines a conjugacy class of subgroups of {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}} and one can show that equivalent covers of ''X'' define the same conjugacy class of subgroups of {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}}. |
|||
==== Examples ==== |
|||
For a covering {{nowrap|''p'' : ''C'' → ''X''}} the group {{nowrap|''p''<sub>#</sub>({{pi}}<sub>1</sub>(''C'', ''c''))}} can also be seen to be equal to |
|||
* The covering <math>q \colon S^1 \to S^1 </math> with <math>q(z)=z^{n}</math> is a normal coverings for every <math>n \in \mathbb{N}</math>. |
|||
* Every simply connected covering is a normal covering. |
|||
=== Calculation === |
|||
the set of [[homotopy class]]es of those closed curves γ based at ''x'' whose lifts ''γ<sub>C</sub>'' in ''C'', starting at ''c'', are closed curves at ''c''. If ''X'' and ''C'' are path-connected, the degree of the cover ''p'' (that is, the cardinality of any fiber of ''p'') is equal to the [[Index of a subgroup|index]] [{{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'') : ''p''<sub>#</sub>({{pi}}<sub>1</sub>(''C'', ''c''))}}] of the [[subgroup]] {{nowrap|''p''<sub>#</sub>({{pi}}<sub>1</sub>(''C'', ''c''))}} in {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}}. |
|||
Let <math>\Gamma</math> be a group, which acts discontinuously on a topological space <math>E</math> and let <math>q: E \rightarrow \Gamma \backslash E </math> be the normal covering. |
|||
A key result of the covering space theory says that for a "sufficiently good" space ''X'' (namely, if ''X'' is path-connected, locally path-connected and [[semi-locally simply connected]]) there is in fact a bijection between equivalence classes of path-connected covers of ''X'' and the conjugacy classes of subgroups of the fundamental group {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}}. The main step in proving this result is establishing the existence of a universal cover, that is a cover corresponding to the trivial subgroup of {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}}. Once the existence of a universal cover ''C'' of ''X'' is established, if ''H'' ≤ {{pi}}<sub>1</sub>(''X'', ''x'') is an arbitrary subgroup, the space ''C''/''H'' is the covering of ''X'' corresponding to ''H''. One also needs to check that two covers of ''X'' corresponding to the same (conjugacy class of) subgroup of {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}} are equivalent. Connected [[cell complex]]es and connected [[manifold]]s are examples of "sufficiently good" spaces. |
|||
* If <math>E</math> is path-connected, then <math>Deck(q) \cong \Gamma</math>.<ref name="Hatcher" /> <math>^{p.72}</math> |
|||
Let ''N''(''Γ<sub>p</sub>'') be the [[normalizer]] of Γ<sub>''p''</sub> in {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}}. The deck transformation group Aut(''p'') is isomorphic to the [[quotient group]] ''N''(Γ<sub>''p''</sub>)/Γ<sub>''p''</sub>. If ''p'' is a universal covering, then ''Γ<sub>p</sub>'' is the [[trivial group]], and Aut(''p'') is isomorphic to {{pi}}<sub>1</sub>(''X''). |
|||
* If <math>E</math> is simply connected, then <math>Deck(q)\cong \pi_1(X)</math>.<ref name="Hatcher" /> <math>^{p.71}</math> |
|||
Let us reverse this argument. Let ''N'' be a [[normal subgroup]] of {{nowrap|{{pi}}<sub>1</sub>(''X'', ''x'')}}. By the above arguments, this defines a (regular) covering {{nowrap|''p'' : ''C'' → ''X''}}. Let ''c''<sub>1</sub> in ''C'' be in the fiber of ''x''. Then for every other ''c''<sub>2</sub> in the fiber of ''x'', there is precisely one deck transformation that takes ''c''<sub>1</sub> to ''c''<sub>2</sub>. This deck transformation corresponds to a curve ''g'' in ''C'' connecting ''c''<sub>1</sub> to ''c''<sub>2</sub>. |
|||
==== Examples ==== |
|||
==Relations with groupoids== |
|||
One of the ways of expressing the algebraic content of the theory of covering spaces is using [[groupoids]] and the [[fundamental groupoid]]. The latter functor gives an equivalence of categories |
|||
* Let <math>n \in \mathbb{N}</math>. The antipodal map <math>g:S^n \rightarrow S^n</math> with <math>g(x)=-x</math> generates, together with the composition of maps, a group <math>D(g) \cong \mathbb{Z/2Z}</math> and induces a group action <math>D(g) \times S^n \rightarrow S^n, (g,x)\mapsto g(x)</math>, which acts discontinuously on <math>S^n</math>. Because of <math>\mathbb{Z_2} \backslash S^n \cong \mathbb{R}P^n</math> it follows, that the quotient map <math>q \colon S^n \rightarrow \mathbb{Z_2}\backslash S^n \cong \mathbb{R}P^n</math> is a normal covering and for <math>n > 1</math> a universal covering, hence <math>Deck(q)\cong \mathbb{Z/2Z}\cong \pi_1({\mathbb{R}P^n})</math> for <math>n > 1</math>. |
|||
:<math>\pi_1: \operatorname{TopCov}(X) \to \operatorname{GpdCov}(\pi_1 X)</math> |
|||
* Let <math>SO(3)</math> be the [[special orthogonal group]], then the map <math>f:SU(2) \rightarrow SO(3) \cong \mathbb{Z_2} \backslash SU(2)</math> is a normal covering and because of <math>SU(2) \cong S^3</math>, it is the universal covering, hence <math>Deck(f) \cong \mathbb{Z/2Z} \cong \pi_1(SO(3))</math>. |
|||
* With the group action <math>(z_1,z_2)*(x,y)=(z_1+(-1)^{z_2}x,z_2+y)</math> of <math>\mathbb{Z^2}</math> on <math>\mathbb{R^2}</math>, whereby <math>(\mathbb{Z^2},*)</math> is the [[semidirect product]] <math>\mathbb{Z} \rtimes \mathbb{Z} </math>, one gets the universal covering <math>f: \mathbb{R^2} \rightarrow (\mathbb{Z} \rtimes \mathbb{Z}) \backslash \mathbb{R^2} \cong K </math> of the [[klein bottle]] <math>K</math>, hence <math>Deck(f) \cong \mathbb{Z} \rtimes \mathbb{Z} \cong \pi_1(K)</math>. |
|||
* Let <math>T = S^1 \times S^1</math> be the [[Torus#Topology|torus]] which is embedded in the <math>\mathbb{C^2}</math>. Then one gets a homeomorphism <math>\alpha: T \rightarrow T: (e^{ix},e^{iy}) \mapsto (e^{i(x+\pi)},e^{-iy})</math>, which induces a discontinuous group action <math>G_{\alpha} \times T \rightarrow T</math>, whereby <math>G_{\alpha} \cong \mathbb{Z/2Z}</math>. It follows, that the map <math>f: T \rightarrow G_{\alpha} \backslash T \cong K</math> is a normal covering of the klein bottle, hence <math>Deck(f) \cong \mathbb{Z/2Z}</math>. |
|||
* Let <math>S^3</math> be embedded in the <math>\mathbb{C^2}</math>. Since the group action <math>S^3 \times \mathbb{Z/pZ} \rightarrow S^3: ((z_1,z_2),[k]) \mapsto (e^{2 \pi i k/p}z_1,e^{2 \pi i k q/p}z_2)</math> is discontinuously, whereby <math>p,q \in \mathbb{N}</math> are [[Coprime integers|coprime]], the map <math>f:S^3 \rightarrow \mathbb{Z_p} \backslash S^3 =: L_{p,q}</math> is the universal covering of the [[lens space]] <math>L_{p,q}</math>, hence <math>Deck(f) \cong \mathbb{Z/pZ} \cong \pi_1(L_{p,q})</math>. |
|||
== Galois correspondence == |
|||
between the category of covering spaces of a reasonably nice space ''X'' and the category of groupoid covering morphisms of {{pi}}<sub>1</sub>(''X''). Thus a particular kind of ''map'' of spaces is well modelled by a particular kind of ''morphism'' of groupoids. The category of covering morphisms of a groupoid ''G'' is also equivalent to the category of actions of ''G'' on sets, and this allows the recovery of more traditional classifications of coverings. |
|||
Let <math>X</math> be a connected and [[Locally simply connected space|locally simply connected]] space, then for every [[subgroup]] <math>H\subseteq \pi_1(X)</math> there exists a path-connected covering <math>\alpha:X_H \rightarrow X</math> with <math>\alpha_{\#}(\pi_1(X_H))=H</math>.<ref name="Hatcher" /> <math>^{p.66}</math> |
|||
Let <math>p_1:E \rightarrow X</math> and <math>p_2: E' \rightarrow X</math> be two path-connected coverings, then they are equivalent iff the subgroups <math>H = p_{1\#}(\pi_1(E))</math> and <math>H'=p_{2\#}(\pi_1(E'))</math> are [[Conjugacy class#Definition|conjugate]] to each other.<ref name=":1" /> <math>^{p.482}</math> |
|||
==Relations with classifying spaces and group cohomology== |
|||
If ''X'' is a connected [[cell complex]] with [[homotopy group]]s {{nowrap|1={{pi}}<sub>''n''</sub>(''X'') = 0}} for all {{nowrap|''n'' ≥ 2}}, then the universal covering space ''T'' of ''X'' is contractible, as follows from applying the [[Whitehead theorem]] to ''T''. In this case ''X'' is a [[classifying space]] or {{nowrap|''K''(''G'', 1)}} for {{nowrap|1=''G'' = {{pi}}<sub>1</sub>(''X'')}}. |
|||
Let <math>X</math> be a connected and locally simply connected space, then, up to equivalence between coverings, there is a bijection: |
|||
Moreover, for every {{nowrap|''n'' ≥ 0}} the group of cellular ''n''-chains ''C''<sub>''n''</sub>(''T'') (that is, a [[free abelian group]] with basis given by ''n''-cells in ''T'') also has a natural '''Z'''''G''-[[Module (mathematics)|module]] structure. Here for an ''n''-cell ''σ'' in ''T'' and for ''g'' in ''G'' the cell ''g'' ''σ'' is exactly the translate of σ by a covering transformation of ''T'' corresponding to ''g''. Moreover, ''C''<sub>''n''</sub>(''T'') is a [[Free module|free]] '''Z'''''G''-module with free '''Z'''''G''-basis given by representatives of ''G''-orbits of ''n''-cells in ''T''. In this case the standard topological chain complex |
|||
<math> |
|||
:<math> \cdots \overset{\partial}{\to} C_n(T)\overset{\partial}{\to} C_{n-1}(T)\overset{\partial}{\to} \cdots \overset{\partial}{\to} C_0(T)\overset{\varepsilon}{\to} \mathbf Z, </math> |
|||
\begin{matrix} |
|||
\qquad \displaystyle \{\text{Subgroup of }\pi_1(X)\} & \longleftrightarrow & \displaystyle \{\text{path-connected covering } p:E \rightarrow X\} |
|||
\\ H & \longrightarrow & \alpha:X_H \rightarrow X \\ |
|||
p_\#(\pi_1(E))&\longleftarrow & p \\ |
|||
\displaystyle \{\text{normal subgroup of }\pi_1(X)\} & \longleftrightarrow & \displaystyle \{\text{normal covering } p:E \rightarrow X\} |
|||
\\ H & \longrightarrow & \alpha:X_H \rightarrow X \\ |
|||
p_\#(\pi_1(E))&\longleftarrow & p |
|||
\end{matrix} |
|||
</math> |
|||
For a sequence of subgroups <math> |
|||
where ''ε'' is the [[augmentation map]], is a [[free resolution|free '''Z'''''G''-resolution]] of '''Z''' (where '''Z''' is equipped with the trivial '''Z'''''G''-module structure, {{nowrap|1=''gm'' = ''m''}} for every {{nowrap|''g'' ∈ ''G''}} and every {{nowrap|''m'' ∈ '''Z'''}}). This resolution can be used to compute [[group cohomology]] of ''G'' with arbitrary coefficients. |
|||
\displaystyle \{\text{e}\} \subset H \subset G \subset \pi_1(X) |
|||
</math> one gets a sequence of coverings <math> |
|||
\tilde X \longrightarrow X_H \cong H \backslash \tilde X \longrightarrow X_G \cong G \backslash \tilde X \longrightarrow X\cong \pi_1(X) \backslash \tilde X |
|||
</math>. For a subgroup <math> |
|||
H \subset \pi_1(X) |
|||
</math> with [[Index of a group|index]] <math> |
|||
\displaystyle[\pi_1(X):H] = d |
|||
</math>, the covering <math> |
|||
\alpha:X_H \rightarrow X |
|||
</math> has degree <math>d</math>. |
|||
== Classification == |
|||
The method of Graham Ellis for computing group resolutions and other aspects of homological algebra, as shown in his paper in J. Symbolic Comp. and his web page listed below, is to build a universal cover of a prospective {{nowrap|''K''(''G'', 1)}} inductively at the same time as a contracting homotopy of this universal cover. It is the latter which gives the computational method. |
|||
== |
=== Definitions === |
||
As a homotopy theory, the notion of covering spaces works well when the deck transformation group is discrete, or, equivalently, when the space is [[locally path-connected]]. However, when the deck transformation group is a [[topological group]] whose topology is not [[discrete topology|discrete]], difficulties arise. Some progress has been made for more complex spaces, such as the [[Hawaiian earring]]; see the references there for further information. |
|||
==== Category of coverings ==== |
|||
A number of these difficulties are resolved with the notion of ''semicovering'' due to Jeremy Brazas, see the paper cited below. Every covering map is a semicovering, but semicoverings satisfy the "2 out of 3" rule: given a composition {{nowrap|1=''h'' = ''fg''}} of maps of spaces, if two of the maps are semicoverings, then so also is the third. This rule does not hold for coverings, since the composition of covering maps need not be a covering map. |
|||
Let <math>X</math> be a topological space. The objects of the [[Category theory|category]] '''<math>\boldsymbol{Cov(X)}</math>''' are the coverings <math>p:E \rightarrow X</math> of <math>X</math> and the [[Morphism (category theory)|morphisms]] between two coverings <math>p:E \rightarrow X</math> and <math>q:F\rightarrow X</math> are continuous maps <math>f:E \rightarrow F</math>, s.t. the diagram |
|||
[[File:Kommutierendes_Diagramm_Cov.png|center|frameless]] |
|||
commutes. |
|||
==== G-Set ==== |
|||
Another generalisation is to actions of a group which are not free. Ross Geoghegan in his 1986 review ({{MR|0760769}}) of two papers by M.A. Armstrong on the fundamental groups of [[orbit space]]s wrote: "These two papers show which parts of elementary covering space theory carry over from the free to the nonfree case. This is the kind of basic material that ought to have been in standard textbooks on fundamental groups for the last fifty years." At present, "Topology and Groupoids" listed below seems to be the only basic topology text to cover such results. |
|||
Let <math>G</math> be a [[topological group]]. The [[Category theory|category]] <math>\boldsymbol{G-Set}</math> is the category of sets which are [[G-set|G-sets]]. The morphisms are [[Group action#Morphisms and isomorphisms between G-sets|G-maps]] <math>\phi:X \rightarrow Y</math> between G-sets. They satisfy the condition <math>\phi(gx)=g \, \phi(x)</math> for every <math>g \in G</math>. |
|||
=== Equivalence === |
|||
Let <math>X</math> be a connected and locally simply connected space, <math>x \in X</math> and <math>G = \pi_1(X,x)</math> be the fundamental group of <math>X</math>. Since <math>G</math> defines, by lifting of paths and evaluating at the endpoint of the lift, a group action on the fiber of a covering, the [[functor]] <math>F:\boldsymbol{Cov(X)} \longrightarrow \boldsymbol{G-Set}: p \mapsto p^{-1}(x)</math> is an [[equivalence of categories]].<ref name="Hatcher" /> <math>^{p.68-70 }</math> |
|||
==Applications== |
==Applications== |
||
[[Image:Rotating gimbal-xyz.gif|thumb|300px|[[Gimbal lock]] occurs because any map {{nowrap|''T''<sup>3</sup> → '''RP'''<sup>3</sup>}} is not a covering map. In particular, the relevant map carries any element of ''T''<sup>3</sup>, that is, an ordered triple (a,b,c) of angles (real numbers mod 2{{pi}}), to the composition of the three coordinate axis rotations R<sub>x</sub>(a)∘R<sub>y</sub>(b)∘R<sub>z</sub>(c) by those angles, respectively. Each of these rotations, and their composition, is an element of the rotation group '''SO'''(3), which is topologically '''RP'''<sup>3</sup>. |
[[Image:Rotating gimbal-xyz.gif|thumb|300px|[[Gimbal lock]] occurs because any map {{nowrap|''T''<sup>3</sup> → '''RP'''<sup>3</sup>}} is not a covering map. In particular, the relevant map carries any element of ''T''<sup>3</sup>, that is, an ordered triple (a,b,c) of angles (real numbers mod 2{{pi}}), to the composition of the three coordinate axis rotations R<sub>x</sub>(a)∘R<sub>y</sub>(b)∘R<sub>z</sub>(c) by those angles, respectively. Each of these rotations, and their composition, is an element of the rotation group '''SO'''(3), which is topologically '''RP'''<sup>3</sup>. |
||
| Line 181: | Line 251: | ||
*[[Galois connection]] |
*[[Galois connection]] |
||
*[[Quotient space (topology)]] |
*[[Quotient space (topology)]] |
||
== Literatur == |
|||
* Allen Hatcher: ''Algebraic Topology''. Cambridge Univ. Press, Cambridge, <nowiki>ISBN 0-521-79160-X</nowiki> |
|||
==Notes== |
|||
* Otto Forster: ''Lectures on Riemann surfaces''. Springer Berlin, München 1991, <nowiki>ISBN 978-3-540-90617-9</nowiki> |
|||
{{reflist}} |
|||
* James Munkres: ''Topology''. Upper Saddle River, NJ: Prentice Hall, Inc., ©2000, <nowiki>ISBN 978-0-13-468951-7</nowiki> |
|||
* Wolfgang Kühnel: ''Matrizen und Lie-Gruppen''. Springer Fachmedien Wiesbaden GmbH, Stuttgart, <nowiki>ISBN 978-3-8348-9905-7</nowiki> |
|||
* Maximiliano Aguilar and Miguel Socolovsky: ''The Universal Covering Group of U(n) and Projective Representations''. Hrsg.: International Journal of Theoretical Physics. Dezember 1999 |
|||
==References== |
== References == |
||
<references /> |
|||
*{{cite book |first=Ronald |last=Brown |author-link=Ronald Brown (mathematician) |title=Topology and Groupoids |year=2006 |publisher=Booksurge LLC |location=Charleston, S. Carolina |isbn=1-4196-2722-8 |url=http://groupoids.org.uk/topgpds.html}} See chapter 10. |
|||
*{{SpringerEOM |
|||
| title=Covering |
|||
| id=Covering&oldid=13627 |
|||
| last=Chernavskii |
|||
| first=A.V. |
|||
}} |
|||
*{{cite book | first1 = Hershel M. | last1 = Farkas | first2=Irwin |last2=Kra| author2-link = Irwin Kra | title = Riemann Surfaces | year = 1980 | edition = 2nd | publisher = Springer | location = New York | isbn = 0-387-90465-4}} See chapter 1 for a simple review. |
|||
*{{cite book | first = Allen | last = Hatcher | author-link = Allen Hatcher | year = 2002 | title = Algebraic Topology | publisher = [[Cambridge University Press]] | isbn = 0-521-79540-0 | url = http://www.math.cornell.edu/~hatcher/AT/ATpage.html}} |
|||
*{{cite book|url=http://138.73.27.39/tac/reprints/articles/7/tr7abs.html|title=Notes on categories and groupoids|first=Philip J.|last=Higgins|publisher=Van Nostrand Reinhold|location=London-New York-Melbourne|series=Mathematical Studies|volume=32|year=1971|mr=0327946|access-date=2008-03-28|archive-date=2007-10-07|archive-url=https://web.archive.org/web/20071007143558/http://138.73.27.39/tac/reprints/articles/7/tr7abs.html|url-status=dead}} |
|||
*{{cite book | first = Jürgen | last = Jost |author-link=Jürgen Jost| title = Compact Riemann Surfaces | year = 2002 | publisher = Springer | location = New York | isbn = 3-540-43299-X}} See section 1.3 |
|||
*{{cite book | first = William | last = Massey | author-link = William S. Massey | title = A Basic Course in Algebraic Topology | year = 1991 | publisher = Springer | location = New York | isbn = 0-387-97430-X}} See chapter 5. |
|||
*{{cite book|last=Munkres|first=James R.|author-link=James Munkres|title=Topology|year=2000|publisher=Prentice Hall|location=Upper Saddle River, NJ|isbn=0131816292|edition=2.}} |
|||
* {{cite journal|last=Brazas|first= Jeremy|title=Semicoverings: a generalization of covering space theory|journal= Homology, Homotopy and Applications|volume= 14 |year=2012|issue= 1|pages=33–63|mr=2954666|doi=10.4310/HHA.2012.v14.n1.a3|arxiv=1108.3021|s2cid= 55921193}} |
|||
* {{cite web|last=Ellis|first= Graham| url=http://hamilton.nuigalway.ie/Hap/www/| title=Homological Algebra Programming}} |
|||
* {{cite journal|last=Ellis|first= Graham|title= Computing group resolutions|journal= [[Journal of Symbolic Computation]] |volume=38 |year=2004|issue= 3|pages= 1077–1118|doi= 10.1016/j.jsc.2004.03.003|doi-access= free}} |
|||
*{{cite book |last=Spanier |first=Edwin|author-link=Edwin Spanier |title=Algebraic Topology |date=1994 |orig-year=1966 |publisher=Springer |isbn=0-387-94426-5}} |
|||
[[Category:Algebraic topology]] |
[[Category:Algebraic topology]] |
||
Revision as of 11:38, 8 June 2022
A covering of a topological space is a continuous map with special properties.
Definition
Let be a topological space. A covering of is a continuous map
s.t. there exists a discrete space and for every an open neighborhood , s.t. and is a homeomorphism for every .

Often, the notion of a covering is used for the covering space as well as for the map . The open sets are called sheets, which are uniquely determined if is connected.[1] For a the discrete subset is called the fiber of . The degree of a covering is the cardinality of the space . If is path-connected, then the covering is denoted as a path-connected covering.
Examples
- For every topological space there exists the covering with , which is denoted as the trivial covering of
- The map with is a covering of the unit circle . For an open neighborhood of an , which has positiv -value, one has: .
- Another covering of the unit circle is the map with for some . For an open neighborhood of an , one has: .
- A map which is a local homeomorphism but not a covering of the unit circle is with . There is a sheet of an open neighborhood of , which is not mapped homeomorphically onto .
Properties
Local homeomorphism
Since a covering maps each of the disjoint open sets of homeomorphically onto it is a local homeomorphism, i.e. is a continuous map and for every there exists an open neighborhood of , s.t. is a homeomorphism.
It follows that the covering space and the base space locally share the same properties.
- If is a connected and non-orientable manifold, then there is a covering of degree , whereby is a connected and orientable manifold.[1]
- If is a connected Lie group, then there is a covering which is also a Lie group homomorphism and is a Lie group.[2]
- If is a graph, then it follows for a covering that is also a graph.[1]
- If is a connected manifold, then there is a covering , whereby is a connected and simply connected manifold.[3]
- If is a connected Riemann surface, then there is a covering which is also a holomorphic map[3] and is a connected and simply connected Riemann surface.[3]
Factorisation
Let and be continuous maps, s.t. the diagram
commutes.
Product of coverings
Let and be topological spaces and and be coverings, then with is a covering.[4]
Equivalence of coverings
Let be a topological space and and be coverings. Both coverings are called equivalent, if there exists a homeomorphism , s.t. the diagram

commutes. If such a homeomorphism exists, then one calls the covering spaces and isomorphic.
Lifting property
An important property of the covering is, that it satisfies the lifting property, i.e.:
Let be the unit interval and be a covering. Let be a continuous map and be a lift of , i.e. a continuous map such that . Then there is a uniquely determined, continuous map , which is a lift of , i.e. .[1]
If is a path-connected space, then for it follows that the map is a lift of a path in and for it is a lift of a homotopy of paths in .
Because of that property one can show, that the fundamental group of the unit circle is an infinite cyclic group, which is generated by the homotopy classes of the loop with .[1]
Let be a path-connected space and be a connected covering. Let be any two points, which are connected by a path , i.e. and . Let be the unique lift of , then the map
- with
If is a path-connected space and a connected covering, then the induced group homomorphism
- with ,
is injective and the subgroup of consists of the homotopy classes of loops in , whose lifts are loops in .[1]
Branched covering
Definitions
Holomorphic maps between Riemann surfaces
Let and be Riemann surfaces, i.e. one dimensional complex manifolds, and let be a continuous map. is holomorphic in a point , if for any charts of and of , with , the map is holomorphic.
If is for all holomorphic, we say is holomorphic.
The map is called the local expression of in .
If is a non-constant, holomorphic map between compact Riemann surfaces, then is surjective[3] and an open map[3] , i.e. for every open set the image is also open.
Ramification point and branch point
Let be a non-constant, holomorphic map between compact Riemann surfaces. For every there exist charts for and and there exists a uniquely determined , s.t. the local expression of in is of the form .[3] The number is called the ramification index of in and the point is called a ramification point if . If for an , then is unramified. The image point of a ramification point is called a branch point.
Degree of a holomorphic map
Let be a non-constant, holomorphic map between compact Riemann surfaces. The degree of is the cardinality of the fiber of an unramified point , i.e. .
This number is well-defined, since for every the fiber is discrete[3] and for any two unramified points , it is: [3]
It can be calculated by:
Branched covering
Definition
A continuous map is called a branched covering, if there exists a closed set with dense complement , s.t. is a covering.
Examples
- Let and , then with is branched covering of degree , whereby is a branch point.
- Every non-constant, holomorphic map between compact Riemann surfaces of degree is a branched covering of degree .
Universal covering
Let be a simply connected covering and be a covering, then there exists a uniquely determined covering , s.t. the diagram

commutes.[4]
Definition
Let be a simply connected covering. If is another simply connected covering, then there exists a uniquely determined homeomorphism , s.t. the diagram

commutes.[4]
This means that is, up to equivalence, uniquely determined and because of that universal property denoted as the universal covering of the space .
Existence
A universal covering does not always exists, but the following properties guarantee the existence:
Let be a connected, locally simply connected, then there exists a universal covering .
is defined as and by .[1]
The topology on is constructed as follows: Let be a path with . Let be a simply connected neighborhood of the endpoint , then for every the paths inside from to are uniquely determined up to homotopy. Now consider , then with is a bijection and can be equipped with the final topology of .
The fundamental group acts freely through on and with is a homeomorphism, i.e. .
Examples
- with is the universal covering of the unit circle .
- with is the universal covering of the projective space for .
- with is the universal covering of the unitary group .[5]
- Since , it follows that the quotient map is the universal covering of the .

The Hawaiian earring. Only the ten largest circles are shown. - A topological space, which has no universal covering is the Hawaiian earring:
- One can show, that no neighborhood of the origin is simply connected.[4]
Deck transformation
Definition
Let be a covering. A deck transformation is a homeomorphism , s.t. the diagram of continuous maps
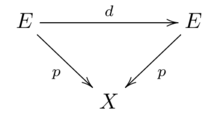
commutes. Together with the composition of maps, the set of deck transformation forms a group , which is the same as .
Examples
- Let be the covering for some , then the map is a deck transformation and .
- Let be the covering , then the map with is a deck transformation and .
Properties
Let be a path-connected space and be a connected covering. Since a deck transformation is bijective, it permutes the elements of a fiber with and is uniquely determined by where it sends a single point. In particular, only the identity map fixes a point in the fiber.[1] Because of this property every deck transformation defines a group action on , i.e. let be an open neighborhood of a and an open neighborhood of an , then is a group action.
Normal coverings
Definition
A covering is called normal, if . This means, that for every and any two there exists a deck transformation , s.t. .
Properties
Let be a path-connected space and be a connected covering. Let be a subgroup of , then is a normal covering iff is a normal subgroup of .[1]
If is a normal covering and , then .[1]
If is a path-connected covering and , then , whereby is the normaliser of .[1]
Let be a topological space. A group acts discontinuously on , if every has an open neighborhood with , such that for every with one has .
If a group acts discontinuously on a topological space , then the quotient map with is a normal covering.[1] Hereby is the quotient space and is the orbit of the group action.
Examples
- The covering with is a normal coverings for every .
- Every simply connected covering is a normal covering.
Calculation
Let be a group, which acts discontinuously on a topological space and let be the normal covering.
- If is path-connected, then .[1]
- If is simply connected, then .[1]
Examples
- Let . The antipodal map with generates, together with the composition of maps, a group and induces a group action , which acts discontinuously on . Because of it follows, that the quotient map is a normal covering and for a universal covering, hence for .
- Let be the special orthogonal group, then the map is a normal covering and because of , it is the universal covering, hence .
- With the group action of on , whereby is the semidirect product , one gets the universal covering of the klein bottle , hence .
- Let be the torus which is embedded in the . Then one gets a homeomorphism , which induces a discontinuous group action , whereby . It follows, that the map is a normal covering of the klein bottle, hence .
- Let be embedded in the . Since the group action is discontinuously, whereby are coprime, the map is the universal covering of the lens space , hence .
Galois correspondence
Let be a connected and locally simply connected space, then for every subgroup there exists a path-connected covering with .[1]
Let and be two path-connected coverings, then they are equivalent iff the subgroups and are conjugate to each other.[4]
Let be a connected and locally simply connected space, then, up to equivalence between coverings, there is a bijection:
For a sequence of subgroups one gets a sequence of coverings . For a subgroup with index , the covering has degree .
Classification
Definitions
Category of coverings
Let be a topological space. The objects of the category are the coverings of and the morphisms between two coverings and are continuous maps , s.t. the diagram

commutes.
G-Set
Let be a topological group. The category is the category of sets which are G-sets. The morphisms are G-maps between G-sets. They satisfy the condition for every .
Equivalence
Let be a connected and locally simply connected space, and be the fundamental group of . Since defines, by lifting of paths and evaluating at the endpoint of the lift, a group action on the fiber of a covering, the functor is an equivalence of categories.[1]
Applications

An important practical application of covering spaces occurs in charts on SO(3), the rotation group. This group occurs widely in engineering, due to 3-dimensional rotations being heavily used in navigation, nautical engineering, and aerospace engineering, among many other uses. Topologically, SO(3) is the real projective space RP3, with fundamental group Z/2, and only (non-trivial) covering space the hypersphere S3, which is the group Spin(3), and represented by the unit quaternions. Thus quaternions are a preferred method for representing spatial rotations – see quaternions and spatial rotation.
However, it is often desirable to represent rotations by a set of three numbers, known as Euler angles (in numerous variants), both because this is conceptually simpler for someone familiar with planar rotation, and because one can build a combination of three gimbals to produce rotations in three dimensions. Topologically this corresponds to a map from the 3-torus T3 of three angles to the real projective space RP3 of rotations, and the resulting map has imperfections due to this map being unable to be a covering map. Specifically, the failure of the map to be a local homeomorphism at certain points is referred to as gimbal lock, and is demonstrated in the animation at the right – at some points (when the axes are coplanar) the rank of the map is 2, rather than 3, meaning that only 2 dimensions of rotations can be realized from that point by changing the angles. This causes problems in applications, and is formalized by the notion of a covering space.
See also
- Bethe lattice is the universal cover of a Cayley graph
- Covering graph, a covering space for an undirected graph, and its special case the bipartite double cover
- Covering group
- Galois connection
- Quotient space (topology)
Literatur
- Allen Hatcher: Algebraic Topology. Cambridge Univ. Press, Cambridge, ISBN 0-521-79160-X
- Otto Forster: Lectures on Riemann surfaces. Springer Berlin, München 1991, ISBN 978-3-540-90617-9
- James Munkres: Topology. Upper Saddle River, NJ: Prentice Hall, Inc., ©2000, ISBN 978-0-13-468951-7
- Wolfgang Kühnel: Matrizen und Lie-Gruppen. Springer Fachmedien Wiesbaden GmbH, Stuttgart, ISBN 978-3-8348-9905-7
- Maximiliano Aguilar and Miguel Socolovsky: The Universal Covering Group of U(n) and Projective Representations. Hrsg.: International Journal of Theoretical Physics. Dezember 1999
References
- ^ a b c d e f g h i j k l m n o p q Hatcher, Allen (2001). Algebraic Topology. Cambridge: Cambridge Univ. Press. ISBN 0-521-79160-X.
- ^ Kühnel, Wolfgang. Matrizen und Lie-Gruppen. Stuttgart: Springer Fachmedien Wiesbaden GmbH. ISBN 978-3-8348-9905-7.
- ^ a b c d e f g h i Forster, Otto (1991). Lectures on Riemann surfaces. München: Springer Berlin. ISBN 978-3-540-90617-9.
- ^ a b c d e f g Munkres, James (2000). Topology. Upper Saddle River, NJ: Prentice Hall, Inc. ISBN 978-0-13-468951-7.
- ^ Aguilar, Maximiliano; Socolovsky, Miguel (December 1999). "The Universal Covering Group of U(n) and Projective Representations". International Journal of Theoretical Physics: 5 Theorem 1.


















![{\displaystyle Y=[0,1]\times \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b566709fb62d0c99d75506726ea4f22fc3f98078)
![{\displaystyle X=[0,1]\times S^{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ecfebcfe87fcb8d16f87d9f6dfecca71bf16af1)





































































![{\displaystyle p_{\#}([\gamma ])=[p\circ \gamma ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0da1f32b69d662c4ca704e03c7f6665cc4c2bbe)











































![{\displaystyle p([\gamma ]):=\gamma (1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeee3b9f2b1a930620d001de56151981af9f4210)









![{\displaystyle p([\gamma .\sigma _{y}])=\gamma .\sigma _{y}(1)=y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6bb60eab8680bfa053e679348dc30132cb28713)



![{\displaystyle ([\gamma ],[{\tilde {x}}])\mapsto [\gamma .{\tilde {x}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fa9846bd74343d9821f1568af6a33b418496a42)

![{\displaystyle \psi ([\Gamma {\tilde {x}}])={\tilde {x}}(1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa3e15841c84e4fbc78e76e0794e15bf868f1877)


![{\displaystyle p(x)=[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24b8773dff8ad19fc5a8f33134a4da367b04fc0c)








































































![{\displaystyle S^{3}\times \mathbb {Z/pZ} \rightarrow S^{3}:((z_{1},z_{2}),[k])\mapsto (e^{2\pi ik/p}z_{1},e^{2\pi ikq/p}z_{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72ebd3752fc18f7e53cc92a583d04ac1b95a75ac)
















![{\displaystyle \displaystyle [\pi _{1}(X):H]=d}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b9159dd8a0e29ba795fe865ddb5140ae95fd675)










