DescriptionLagrange simple.svg	English: derivative of https://en.wikipedia.org/wiki/File:Lagrange_simple.jpg
Date	7 August 2012
Source	Own work based on: Lagrange simple.svg en:File:Lagrange simple.jpg
Author	Original: Jacobmelgaard   Vector: Zerodamage
SVG development InfoField	The SVG code is valid.   This oversized trigonometry was created with Inkscape.    This trigonometry uses embedded text that can be easily translated using a text editor.

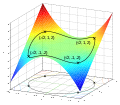
The graph was made in Matlab with the following source code

% Function data
[X,Y] = meshgrid(-2:0.1:2, -2:0.1:2);
Z = (X.^2).*Y;

% Constraint data
t = -pi:0.01:pi;
xc = sqrt(3)*cos(t);
yc = sqrt(3)*sin(t);
zc = xc.^2 .* yc;

% Plot graph and constraint
figure();
surface = surfc(X,Y,Z);

hold on;
plot3(xc, yc, zc, 'k', 'LineWidth', 2);
plot3(xc, yc ,-10*ones(1,length(t)), 'k', 'LineWidth', 1);
set(gcf, 'Color', [1 1 1]);
set(gcf, 'Position', [46 107 767 682]);
% Axis labels
text(0.2, -3, -10, 'x');
text(2.5, -.5, -10, 'y');
text(-2.4, -2, 0, 'z');

% Annotations of the max and min points
% Point indicating max #1
plot3(sqrt(2), 1, 2, 'kx', 'MarkerSize', 14, 'LineWidth', 2);
plot3(sqrt(2), 1, -10, 'kx', 'MarkerSize', 10, 'LineWidth', 2);
text('Interpreter', 'latex',...
        'String', '$$(\sqrt{2}, 1, 2)$$',...
        'Position', [1.1 .1 2.1],...
        'FontSize', 20);
% Point indicating max #2
plot3(-sqrt(2), 1, 2, 'kx', 'MarkerSize', 14, 'LineWidth', 2);
plot3(-sqrt(2), 1, -10, 'kx', 'MarkerSize', 10, 'LineWidth', 2);
text('Interpreter', 'latex',...
        'String', '$$(-\sqrt{2}, 1, 2)$$',...
        'Position', [-1.6 .1 2.1],...
        'FontSize', 20);
% Point indicating min #1
plot3(sqrt(2), -1, -2, 'kx', 'MarkerSize', 14, 'LineWidth', 2);
plot3(sqrt(2), -1, -10, 'kx', 'MarkerSize', 10, 'LineWidth', 2);
plot3(0,1,-3,'kx')
text('Interpreter', 'latex',...
        'String', '$$(\sqrt{2}, -1, -2)$$',...
        'Position', [.5 -.8 -1.4],...
        'FontSize', 20);
% Point indicating min #2
plot3(-sqrt(2), -1, -2, 'kx', 'MarkerSize', 14, 'LineWidth', 2);
plot3(-sqrt(2), -1, -10, 'kx', 'MarkerSize', 10, 'LineWidth', 2);
text('Interpreter', 'latex',...
        'String', '$$(-\sqrt{2}, -1, -2)$$',...
        'Position', [-1.9 -.8 -1],...
        'FontSize', 20);
hold off;
shading interp;
view([25 18]);
%plot2svg must be retrieved from http://www.zhinst.com/blogs/schwizer/
plot2svg;

Corresponding Mathematica code:

Block[{x, y, f = #^2 #2 &, g = #^2 + #2^2 &, c = 3},
 sol = With[{max = MaxValue[{f[x, y], g[x, y] == c}, {x, y}]},
   Solve[{f[x, y] == max, g[x, y] == c}, {x, y}, Reals]
   ];
 Show[
  Plot3D[f[x, y], {x, -2, 2}, {y, -2, 2}, Mesh -> {{c}}, 
   MeshFunctions -> g, PlotRange -> All, Boxed -> False, 
   AspectRatio -> 1, PlotPoints -> 30, MeshStyle -> Cyan, 
   PerformanceGoal -> "Quality", ColorFunction -> "DeepSeaColors"],
  Graphics3D[{Red, PointSize[Large], Point[{x, y, f[x, y]} /. sol]}]
  ]
 ]

This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.

You are free:

• to share – to copy, distribute and transmit the work
• to remix – to adapt the work

Under the following conditions:

• attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
• share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.

https://creativecommons.org/licenses/by-sa/3.0CC BY-SA 3.0 Creative Commons Attribution-Share Alike 3.0 truetrue